UK Home Office Scientific Advisory Branch debunked the Campaign for Nuclear Disarmament, British Medical Association, and Duncan Campbell's propaganda on nuclear weapons effects

1974 edition of the "Nuclear Weapons" civil defence handbook (compare it to the original 1956 edition, post Operation Hurricane, but pre-Operation Buffalo, linked here): based on secret nuclear test data (particularly work done by George R. Stanbury and Frank H. Pavry at Operations Hurricane and by AWRE's Dr Loutit and Dr Scott Russell on fallout from the Buffalo-2 surface burst in Australia), it covered up its detailed research basis and was easily "ridiculed" (despite being well founded on fact) by CND's Phil Boswell in "Civil Defence: the Cruellest Confidence Trick".

Firestorms in modern cities debunked 1964
This post will correlate the originally secret (now declassified) UK National Archives reports upon which the book was based with the specific facts given on civil defence countermeasures.
Nuclear Weapons had three editions during the cold war (1956, 1959 and 1974). The first edition is the best organized as we previously discussed, with the 1959 and 1974 editions being obfuscated by a more complex, broken-up structure of chapters (e.g., fallout radiation information is dispersed in a disorganized manner between chapters 1, 2, 3, 8, 9, 10 and 11, with other effects like initial radiation, blast, cratering, and thermal in chapters 4-7). The original 1956 edition is more straightforward, with all the fallout radiation well organized and better illustrated in chapter 3 (the 1956 illustrations of the protection factors against fallout in buildings of different sizes and in different kinds of trench shelters were removed from the 1959 and 1974 editions). In addition, while chapters 1-10 have the same titles in the 1959 and 1974 editions, the final chapter in the 1959 edition, Chapter 11: Summary of Methods of Protection and Decontamination for the Individual, was removed in its entirety from the 1974 edition; that 1959 edition chapter showed on page 59 that to avoid ignition of bedspreads and curtains, they can be made fireproof with a fire-retardant solution (which allows fabric to smoke when exposed to an intense thermal pulse, without allowing sustained ignition once the thermal pulse ends):
"Suitable solutions for household use are 3 lb boric acid plus 2 lb sodium phosphate (or, alternatively, 3 lb borax plus 2 lb boric acid) dissolved in 3.5 gallons of water. Curtains and fabrics should be thoroughly soaked in the solution and the excess liquid squeezed out before they are rinsed and dried."
It also states on page 61:
"Curtains or sheets should be tacked over broken windows to keep gross amounts of fallout from being blown into the rooms. ... If dust was visible later in any room, it should be swept and dumped outside."
It explains that sustained skin contact with fallout causes delayed beta burns on page 62, adding:
"Contaminated clothing can be cleaned to a very considerable extent (almost complete removal of fallout particles)" by "an efficient vacuum cleaner" or "5 minutes in a washing machine or 5 minutes vigorous stirring" in water. This was proved by clothing decontamination trials at British land detonation tests and at the Nevada nuclear tests of Operation Jangle in 1951, as reported in weapon test report WT-347. The low contamination risk for clothing in a land burst nuclear explosion was proved at those tests in 1951:
"Four hours after the surface detonation, eight teams of men worked for a period of one hour in the contaminated areas. Five days after the underground detonation, one team walked and one team walked and crawled through the 10 to 500 milliroentgen per hour area, downwind from Ground Zero. The walking team traveled approximately 1/2 mile in 1/2 hour. The walking and crawling team crawled ten yards in the 300 milliroentgen per hour zone. ... Of protective clothing worn by men after the surface detonation, gloves and boots worn into areas near Ground Zero were the most highly contaminated, giving readings ranging from .01 to 9 mr/hr at six inches when monitored 26 hours after the detonation. Contamination of underclothing was negligible. Of the clothing worn into the contaminated area produced by the underground detonation, the maximum reading was 3.7 mr/hr. The men who crawled received only 2 to 4 mr from their clothing while receiving a total dosage of 1 to 2 roentgens, as measured by film badges which recorded radiation from both the clothing and the ground ... the level of radiation due to dust on clothing throughout the tests was negligible." - nuclear weapons test report WT-401, 1952.
The deletion of this final chapter on defence from the 1974 edition was a mistake. Exactly the same thing occurred with the American manual by Glasstone and Dolan, The Effects of Nuclear Weapons, Chapter 12 Principles of Protection which had been in the 1957 and 1962/4 editions was removed in its entirety from the final 1977 edition. This marked a complete change from Glasstone's stated objective on page 1 of the 1950 edition, titled The Effects of Atomic Weapons, which was making the case publically for civil defence.
If you present information on effects of nuclear weapons for a range of yields, CND inspired prejudice ensures that the public will look only at the effects of the highest yield given, 10-20 megatons, and then exaggerate the problem as a means to avoid confronting the facts realistically. By analogy, when seatbelts were introduced, people who did not want to wear them argued that they would produce a false sense of security and encourage people to drive faster, and would be hinder escape if the petrol tank exploded. The lesson is that it is necessary to focus on the most probable dangers, and to reduce them, instead of inventing spurious arguments that do not apply in the majority of cases.
The popular anti-nuclear propaganda works by a focus on large megaton yields which won't fit into missiles. A one megaton yield requires nearly a ton of bulky warhead if the weapons are cost effective, and that won't fit in the Trident SLBM, and only one such weapon can fit in a Minuteman class ICBM. Even the colossal and now obsolete American Titan II missile, big enough to put a small satellite into orbit, could only launch a single nine megaton warhead. In reality, the majority of warheads are submegaton. (As the tragic fate of MH17 proved last year, Russian cold war BUK ground-to-air missiles can shoot down aircraft carrying larger bombs.) The point is, anti-nuclear biased propaganda has gone so far into lunacy that only the least probable, largest yield nuclear weapon, is considered in an effort to debunk civil defence by populist scare mongering. Most physicists are still duped into the delusion that, to use an analogy, home fire insurance is no use because if your house catches fire, you and your family will be overkilled by invisible carbon monoxide gas, hot dust fumes, radiant heat, convective flame heat, and even if you and your family survive, you will be horribly mutated by terrible burns, brain and lung damage by fumes, etc.
Moving back to the nuclear bomb, the Trident and ICBM protected second strike capability is an anti-accident countermeasure, removing the necessity to escalate in case of accidents or mis-judgements, and removing the need to "launch on warning" (which was actually the "fail-safe" threat of Stanley Kubrick's anti-nuclear propaganda film). So, as with Hitler's non-use of 12,000 tons of tabun nerve gas in WWII, even if war breaks out with another nuclear power, we can continue to deter escalations to full-scale strategic nuclear attacks by the threat of the protected second-strike capability, just as our gas masks, mustard gas stockpile and proof-tested anthrax cattle cakes in WWII helped to deter Hitler's use of WMDs like tabun and sarin nerve gas (which he could have loaded into the V1 cruise missiles and V2 rockets). What about improvised terrorist nuclear weapons and accidental (primary stage or one-point) bomb explosions? The existence of a protected second-strike capability is a deliberate and successful de-escalator of accidents, a technique to prevent escalation. As a result, the most likely nuclear explosions are low yield terrorist attacks.
Even "accidental nuclear explosions" (bombs dropped by accident) are far more likely to go off with a relatively low yield than at their maximum yield, due to safety measures such as one-point implosion safety which ensures that in an accident the nuclear yield is trivial in comparison to the conventional explosive yield, which itself is impact and fire resistant, requiring a special type of explosive detonator to set it off (in addition, the capacitor charging, neutron initiator tube timing, tritium boost gas release into the core, etc. must all occur before it is even possible for a firing switch to "accidentally" set off a full yield explosion in an impact, contrary to ignorant annotations on a declassified document quoted by Eric Schlosser's Command and controlC book). Tests of deliberately burned nuclear weapons proved that there is no significant hazard. Nobody in the media panicked when a huge dose of polonium-210 contaminated a trail around London in 2006 after being placed into the tea of Mr Litvinenko by alleged agents of Mr Putin, a dose which was so massive that it caused not merely increased long-term cancer risks but actual short-term radiation damage resulting in organ failure.
The newspapers and TV did not run scare stories about the (small) risks from spilled tea on tables, sweat and exhaled air from someone contaminated, and so on. Nor do they do so when alpha emitter Am-210 is burned in household smoke detector fires. The reason of course is that there is no profit from scare-mongering in these cases. Mr Joe Public can see that whatever the risk, there's also a very real risk of being run over by a taxi or bus, hit by a cyclist, mugged, or being exposed to pollution in London. If a smaller hazard existed from a burning nuclear weapon in an accident, the story would be very different, because many people have been duped or brainwashed by one-sided propaganda into the notion that giving up nuclear knowledge and going back to the conventional weapons era of world wars, is a good cause.
Polonium-210 incidentally is used with beryllium as a neutron initiator for primitive nuclear weapons like the 1945 designs, so the very fact it was available in lethal quantities in London in 2006 after being smuggled in without detection goes to prove that the triggering of a smuggled nuclear weapon is not beyond the realms of possibility. The people who smuggled Russian polonium-210 into London to commit murder of a Russian dissident are hardly likely to be the kind of people you would trust. They might as well as sold it to terrorists.
The origins of British blast effects research for nuclear weapons
The very first assessments of air blast from nuclear weapons were done in London in 1941, during World War II, long before Los Alamos was set up in New Mexico, by physicists Penney and Taylor at the Civil Defence Research Committee (RC) of the Ministry of Home Security, London (wartime version of the Home Office, with responsibility for civil defence). Examples of these reports are RC-210 from early 1941, Sir G. I. Taylor's The Formation of a Blast Wave by a Very Intense Explosion (which was published in 1950, see link here with an extra portion comparing the prediction to the Trinity blast data) and Lord William G. Penney's October 1941 RC-260, On the Development of Suction behind a Blast Wave in Air, and the Energy Dissipation, and his co-authored December 1941 RC-286, Note on the Rate of Dissipation of the Energy of the Blast Wave.
"... the radii of ... damage ... for ground burst bombs would be increased possibly by as much as 30 % if the weapon were air burst at about the optimum height." - Nuclear Weapons, 1959, paga 7.11, p33.
This claim is well founded (see British versus American nuclear test data curves below) but as the British Medical Association and anti-nuclear group SANA (Scientists Against Nuclear Arms) publicised in 1983, it conflicts with the American data showing an increase by up to 50% in blast damage ranges for a few psi. However, page 6, para 1.22 in the same book makes it clear that the optimum blast damage height of burst is 1,000 ft for a 20 kt air burst (well above the fireball radius, thus averting intense fallout), which by the cube-root scaling law is equivalent to a 1 kt air burst at 368 feet, which as the graph below shows, optimises very high overpressures, and only causes about a 30% increase over ground burst radii for low pressures. Where the BMA and SANA go wrong is in their unstated but evident prejudice that capitalist America is always right and imperialist Britain is always wrong, in any dispute:
Above: British blast wave nuclear test data from William G. Penney, compared to Glasstone and Dolan, Effects of Nuclear Weapons (i.e. the unclassified summary of data in the secret report series DASA-1200). Penney published a summary of the British height of burst curves in 1970 in his 68 pages long analysis of the nuclear destruction of modern buildings in Hiroshima and Nagasaki (using British nuclear test data to determine the shielding effect of blast energy by damage to buildings), but the original data report by AWRE remains classified and retained from public display in the UK National Archives (reference ES 12/19, Comparison of British air blast with nuclear weapons blast phenomena: Part 3; variation of air blast on the ground with height of burst; AWRE Foulness, report AWRE/DASA/1200/3, Retained by Department under Section 3.4; Retained in departments on security or other specified grounds).
Blast wave attenuation by damage done in a modern city: hard facts from actual experimentation
The blast attenuation curve for Hiroshima is the effect of buildings absorbing blast wave energy. In a city, the blast wave is attenuated rapidly due to the buildings, contrary to Glasstone's data for blast over unobstructed desert; an effect proved by Penney in his comparison of blast over concrete, dark desert sand, and the cities of Hiroshima and Nagasaki. Energy must always be conserved, but this is traditionally ignored by the American manuals on the capabilities of nuclear war. Energy is removed from the blast wave by the following four fundamental processes in a city:
1. SEISMIC WAVES WITHIN THE BUILDING MATERIAL. Some of the blast energy is transformed into a seismic wave in the concrete or steel of the building material, similar to a ground shock wave. This is however only a relatively small use of blast energy. (Traditionally, a "no-go theorem" is invented by dogmatic, politically biased groupthink, whereby you ignore all sources of blast energy loss due to buildings by just calculating the trivial energy loss caused by sending a shock wave into a building frame, prove it to be trivial, then "close down the argument" about blast energy loss, while always ignoring the mechanisms that absorb most of the blast energy! This kind of "reductionist fallacy" occurs everywhere.)
2. DAMAGE TO BUILDING. Breaking the thick large glass windows and wall panels of modern city buildings absorbs some blast wave energy (quite apart from the seismic coupling mentioned above). This energy is used in breaking the chemical bonds in the materials, like the crystalline lattice of the glass. This energy ends up as a small rise in temperature of the debris.
3. KINETIC ENERGY OF DEBRIS ACCELERATED BY THE BLAST WINDS. Once windows are broken, the winds behind the blast front accelerate the fragments to some extent. The peak wind velocity behind a 1 psi peak overpressure blast wave is 40 miles per hour, but the blast wave has passed at supersonic velocity before the debris has been accelerated to 40 mph. Nevertheless, this can be very important in absorbing the energy of the drag or dynamic pressure of the blast wave. (Blast walls, for instance, work by deflecting and stopping the blast winds. If a building wall survives the blast wave, it does the same job of stopping the blast winds/dynamic pressure and has a shielding effect.).
4. ENERGY OF OSCILLATION OF BUILDING AS A WHOLE. (See graph here which is from Professor Bridgman's 2001 unfortunately limited distribution book on the physics of nuclear weapons effects.) Apart from the energy used in sending a seismic wave through the building, and apart from the energy used in breaking doors and windows or panels and apart from the energy used in accelerating the resulting debris fragments, there is another use of energy that absorbs energy from the blast wave: this is the oscillation of the building as a whole. The whole building oscillates like a massive tuning fork, at its resonate frequency, after being hit by the blast loading. The amplitude of the blast wave determines the amplitude of the oscillation of the centre of mass of the building. If a force (i.e. net loading pressure times area), F moves the centre of mass of a building distance x, the energy absorbed by the building is simply E = Fx. There is nothing complex here. Apart from a seismic wave being sent through the building, blast energy is also absorbed through the building suffering cracks to glass and panels, the blast wind energy used to accelerate fragments of the resulting debris, and the overall vibration of the whole building which can absorb lots of blast energy!
The first discussion of blast energy depletion due to cumulative energy use (physical work done, E = Fx) to buildings in a city is in Hans A. Bethe's 13 August 1947 Los Alamos report LA-1021, Volume VII, Blast Wave, Part II, Chapters 5 through 10, which contains Chapter 10 by John von Neumann and Fredrick Reines, The Mach Effect and the Height of Burst, section 10.1 General Considerations on the Production of Blast Damage (pages X-1 to X-2):
"As to the detailed description of the target ... the structures ... have the additional complicating factor of not being rigid. This means that they do not merely deflect the blast wave without absorbing energy from it, but take a tariff on the blast at each reflection.
"In addition to be weakened by destroying structures, the blast wave may, of course, also be weakened by imparting kinetic energy to the debris. The removal of energy from the blast as it does its job decreases the blast pressure at any given distance from the point of detonation to a value somewhat below that which it would have in the absence of dissipative objects ... The presence of such dissipation makes it necessary to consider somewhat higher values of the pressure than would be required if there were only one structure set by itself on a rigid plane."
"... the structures ... have the additional complicating property of not being rigid. This means that they do not merely deflect the shock wave, but they also absorb energy from it at each reflection.
"The removal of energy from the blast in this manner decreases the shock pressure at any given distance from the point of detonation to a value somewhat below that which it would have been in the absence of dissipative objects, such as buildings."
This was removed from future editions, and replaced by a false claim (defying the conservation of energy) that blast waves effects can be increased in cities by reflection! Actually, the reflection process that enhances peak overpressure does not violate conservation of energy in the blast wave: the mechanism for the increased overpressure upon reflection by a rigid surface is simply that: (a) while the blast rebounds, it temporarily travels through itself, temporarily doubling the peak overpressure (this effect ceases when the blast wave has moved away from the surface, and is restored to the normal pressure) and (b) the stopping of the dynamic (wind) pressure by a rigid, perfectly reflecting wall simply converts the dynamic pressure into overpressure, so you are not getting something for nothing, you're just changing one thing (dynamic pressure) into another thing (overpressure).
Since both overpressure and dynamic pressure contribute to blast effects, it is simply not automatically true that blast reflection enhances the net blast effect: it enhances overpressure near the reflecting surface, but at the expense of the dynamic pressure. If you get a massive reflection factor due to such reflection, some of the energy diffracts upward as the blast moves over the structure, and it doesn't all diffract back down on the opposite side after passing over. Some energy is always lost. If you shout in a built up area, the sound is attenuated faster than over unobstructed ground, despite the diffraction of some of the sound waves around structures. Diffraction is not 100% energy efficient, due to both energy losses upward to the sky and to absorption of energy by structures. This isn't "speculative guesswork": it's down to the conservation of energy, one of the strongest empirical facts of nature.
Above: George A. Coulter's 1980 U.S. Army report on city shielding of blast waves, Shielding from blast effects - 1/8th scale model city complex, AD090701 (invalidating unobstructed Nevada desert blast data) concluded on page 80 with the recommendation to add a blast shielding correction to existing computer models of nuclear weapon blast waves. This went unheeded, just like Penney's 1970 paper, which was cited in the blast phenomena bibliography in the 1977 edition of Glasstone and Dolan, but otherwise ignored. It is a ridiculous situation, since the smaller attenuation of peak overpressure by vaporization of fog and rain droplets was included in the 1957 Capabilities of Nuclear Atomic and 1972 Capabilities of Nuclear Weapons.
Professor Bridgman (Introduction to the Physics of Nuclear Weapons Effects, DTRA, 2001) considers a building with an exposed area of 163 square metres, a mass of 455 tons and natural frequency of 5 oscillations per second, and finds that a peak overpressure of 10 psi (69 kPa) and peak dynamic pressure of 2.2 psi (15 kPa) at 4.36 km ground range from a 1 Mt air burst detonated at 2.29 km altitude, with overpressure and dynamic pressure positive durations of 2.6 and 3.6 seconds, respectively, produces a peak deflection of 19 cm in the building about 0.6 second after shock arrival. The peak deflection is computed from Bridgman's formula on p. 304: deflection at time t is given by: xt = [A/(fM)] {integration symbol} [sin(f t)] (Pt + CDqt) dt metres, where A is the cross-sectional face-on area of the building facing to the blast (e.g., 163 square metres), f is the natural frequency of oscillation of the building (e.g., 5 Hz), M is the mass of the building, Pt is the overpressure at time t, CD is the drag coefficient of the building to wind pressure (CD = 1.2 for a rectangular building), and qt is the dynamic pressure at time t. This 19 cm computed maximum deflection allows us to estimate how much energy is permanently and irreversibly absorbed from the blast wave by a building. If the effective loading pressure (overpressure and dynamic pressure combined) on the building for the first 0.5 second is equal to 12 psi (83 kPa) then the mean force on the building during this time is 13 million Newtons, and the energy absorbed by the building from the blast wave (reducing the potential of the blast to cause further destruction at greater radial distances) is simply:
E = Fx = 13,000,000*0.19 = 2.6 MJ.
Although you might expect some overpressure to diffract downwards as the energy is depleted near ground level, diffracted blast pressures are lower than incident blast pressures. In any case, dynamic pressure is a directional (radial) wind effect which does not diffract downwards like the overpressure does. Hence, blast energy loss from the wind (dynamic) pressure cannot be compensated for by downward diffraction. This is why shallow open trenches provided protection against wind drag forces at nuclear tests in the 1950s, although the overpressure component of the blast did diffract into them.
The Home Office Scientific Advisory Branch blast expert was Frank H. Pavry, who like Penney had been to Hiroshima and Nagasaki to assess the blast effects there, and had also attended the 1952 British nuclear test, Operation Hurricane, where he exposed 15 WWII 1939-designed Anderson civil defence shelters, proving their utility against nuclear blast. (A data summary for Anderson shelters at Hurricane is here and here. Note that due to local conditions they used easily blasted sandbags, not packed earth cover, which provides additional blast shielding by the strong "earth arch" effect.) Pavry in 1957 summarized the secret data on blast height of burst effects, including the thermal effects from the precursor, in Report of a course given to university physics lecturers at the Civil Defence Staff College 8-11 July 1957, UK National Archives document HO 228/21. For example, the 1957 edition of TM 23-200, Capabilities of Atomic Weapons, shows that the classical Rankine-Hugoniot equations relating overpressure and dynamic pressure are false when blast energy is absorbed by the sand-storm "precursor" blast effect (Figures 2-9A, 2-10A, 2-13 and 2-13): for a 1 kt nuclear burst at 300 ft height, the ideal surface 15 psi peak overpressure range is reduced by from 315 yards to 210 yards by the precursor, while the peak dynamic pressure is increased at 200 yards range from 20 psi for an ideal surface to 60 psi for the precursor. In other words, the blast wave parameters are very susceptible to the effect of loading by sand and dust, sent into the air near the ground by the thermal pulse. (Pavry also proved the nuclear blast protection of the London underground tube system, in 1963. In addition to Pavry, WWII shelter expert Leader-Williams assessed the nuclear test data and applied it to prove how to minimise casualties in a nuclear war.)
This continuing British secrecy is worse for EMP, fallout, and thermal burns and fire effects (see previous post for thermal burns exaggerations versus real data), fully explaining why the public is so deluded on nuclear weapons effects today. CND anti-nuclear biased propaganda supporters like Phil Bolsover and Duncan Campbell simply assumed that misleading American data disproved British civil defence, which - because the supporting nuclear test evidence was secret - was assumed to be badly informed guesswork. The conflict between the British and American height of burst curves is down to some of the thermal energy being incorporated into the blast, increasing the effective blast yield. This effect is easy to compute mathematically, because it's the same kind of calculation used to compute blast waves from the neutron bomb, where the neutrons heat up the air prior to the blast wave travelling through it and picking up energy from the hot air. So what you're basically doing is adjusting the effective blast yield of the air burst nuclear weapon, by adding to it a fraction of the thermal radiation energy, namely that intercepted by the ground prior to the arrival of the air blast at the location of interest. This greatly enhances the purely hydrodynamic Mach region blast reflection effect. (In a surface burst, most of the thermal rays run parallel to the ground and are not intercepted by it, so there negligible enhancement of the blast wave by the thermal flash.)
Penney obtained very good blast overpressure data for British free air bursts of about 1 kt and 15 kt yield in Maralinga, which were high enough above the ground to prevent the desert sand being popcorned (the "precursor" blast wave), so that thermal effects were isolated and the surface hot air heating contribution to the blast wave could be correlated with the data from a series of scaled low yield AWRE conventional TNT air bursts over a concrete heat-reflecting surface in England. (This explains the fact that the British nuclear weapons handbook shows less of a blast enhancement for air bursts than Glasstone does, a trivial issue that led to complete nonsense from Phil Bolsover, Duncan Campbell, and the Marxist militant group within the a political trade union called the British Medical Association, which produced an ill-informed report on nuclear war in 1983, which exploited Thatcher's continuing secrecy on British nuclear weapon test effects.) The April 1980 Kaman Sciences Corporation Handbook for Nuclear Weapons Effects under Arctic Conditions, AD-A197814, in Figure 2-17 confirms the validity of the Penney's UK AWRE (Atomic Weapons Research Establishment) blast wave height-of-burst analysis, by comparing the AWRE curves to conventional explosive data from three American laboratories (Naval Ordnance Laboratory, Sandia Corporation and Ballistic Research Laboratories):
Although full three-dimensional computer calculations of blast waves, including Mach wave formation, have been done, the theoretical assumptions behind the theory used in the calculations can be disputed in the light of the actual nuclear explosion and TNT data. The controversial aspect of theoretical calculations is the theory used for the Mach region reflection enhancement. As stated above, when a blast wave hits a rigid surface at normal incidence, the peak overpressure is increased due to the reflected blast passing back through itself (doubling the overpressure, temporarily, until the reflection process is finished) and an additional increase also occurs due to the stopping of the dynamic (wind) pressure, which gets converted into overpressure. However, energy is conserved, so the enhancement by purely hydrodynamic means comes at a price, for example, a reduced duration of the reflected overpressure blast; and some of the blast wave energy in perfect reflection ends up being reflected back towards ground zero, some goes upward, and only a portion diffracts around the rigid object to continue on the original trajectory. This is even before energy absorption (non-rigid structures) processes are considered.
John von Neumann came up with the first theory to predict the oblique or Mach stem blast "reflection" effect in his 1943 report for the U.S. Bureau of Ordnance, Oblique Reflection of Shocks, Explosives Research Report 12, but this "three shock" (Mach "Y" stem) theory tended to exaggerate the pressures observed for nuclear weapons even in ideal conditions on unobstructed deserts. An alternative theory was that the Mach region overpressures for air bursts should be similar to those in a surface burst (since the Mach wave is a composite of incident and reflected pressures, as occurs for the hemispherical blast in a surface burst), with a slight enhancement for the fact that energy lost in surface burst cratering is available for blast. However, this theory underestimated the observed pressures. It now seems clear that the latter theory is useful, if a simple allowance for thermal heating of the surface is made. Up to half the thermal yield of an air burst can be absorbed by the ground, and since only a small fraction of the blast wave travels near the ground, the thermal heating of the surface by an air burst effect can give a considerable boost to the effective blast yield to use in predicting peak overpressures over the ground.
The fallout threat assessment
Because the fallout patterns from British nuclear tests were irregular in shape, Britain never got into the American muddle of using idealized cigar shaped "fallout predictions" (these originated from the fact that the first ever American surface burst test, 1.2 kiloton Jangle-Sugar in 1951, occurred in a simple wind structure, thus setting up a dogma of simplistic analysis). The British basis for fallout area predictions is explained by George R. Stanbury's 1959 report, CD/SA 101, Downwind fallout area from groundburst megaton explosions, which compares the fallout areas given by Dr Frank H. Shelton in his June 1959 testimony to the Congressional Hearings on the Biological and Environmental Effects of Nuclear War, with Glasstone's 1957 Effects of Nuclear Weapons, and with the November 1957 Confidential-classified American TM 23-200, Capabilities of Atomic Weapons (which by 1959 was in British hands, part of an exchange deal). Stanbury notes that Shelton's data was probably quoted directly from TM 23-200. He also notes that the Confidential TM 23-200 gives smaller fallout areas than Glasstone's book. The figures for fallout areas which Stanbury chose to go into the 1959 edition of Nuclear Weapons were from Glasstone 1957, not TM 23-200, however only areas are given, which are less sensitive to wind conditions than distances. This is because the fallout contours generally become narrower when the wind speed is increased, so the area covered is often the same (however this is not always true, since a very strong wind can spread out the fallout over such a large area that the very high dose rate contours which occur in light winds disappear completely).
For example, Capabilities of Atomic Weapons, TM 23-200 (1957) Figures 4-15B and 4-16B for a 1 megaton fission surface burst in a simple 15 knots wind pattern gives at 1 hour a dose rate of 3,000 R/hr extending 12.5 statute miles downwind, with a width of 3.0 miles. This can be directly compared to Glastone, Effects of Nuclear Weapons 1957, Table 9.71, which states the downwind distance for this case (15 statute miles per hour, which is nearly 15 knots since a nautical mole is 6076 feet, compared to 5280 ft for a statute mile) is 22 statute miles, and the width is 3.1 miles. Thus, Glasstone shows a much larger fallout area than the classified book. According to Figure 4-4B in Capabilities of Atomic Weapons, TM 23-200 (1957), for a 1 megaton fission weapon and 15 knots wind the 1 hour reference time 3,000 R/hr fallout contour covers an area of 26 square miles, but Stanbury, following Glasstone 1957, selects a figure over twice that large, 54 square miles, shown in Table 15 of the 1959 Nuclear Weapons (for this small distance from ground zero, the fallout is soon deposited so that 3,000 R/hr at 1 hour is equivalent to 300 R/hr at 7 hours after detonation, due to the rapid -1.2 power of time decay rate of fallout). This figure is modified to 20 square miles in Table 13 in the 1974 edition, purely because of the decision to use a 50% fission yield for fallout from thermonuclear weapons.
Fallout of 3,000 R/hr at an effective arrival time of 1 hour gives 8,085 R during the first two days, which is reduced to 8,085/40 = 202 R in a typical British brick house refuge room with windows blocked (protection factor 40) or 40 R or less in an outdoor earth-covered trench shelter (protection factor 200 or more). At this time, 48 hours after detonation, the dose rate has fallen by natural radioactive decay from the 1 hour level of 3,000 R/hr to just 30 R/hr, which would allow evacuation towards the upwind or cross-wind direction, as organized by the Cold War Civil Defence Corps for all "Z zone" areas where the dose rate at 48 hours is above 10 R/hour, as documented in Manual of Civil Defence, Radioactive Fallout: Provisional Scheme of Public Control.
People could return even to this most highly contaminated "hotspot" at 14 weeks after detonation, when the dose rate would be down to just 0.3 R/hour and still decaying, a factor of 10,000 times smaller than the 3,000 R/hour at 1 hour. Contrast this 20 square miles area of inconvenient fallout hazard from a 50% fission 1 megaton surface burst (requiring merely a 48 hour indoor stay and the evacuation for 3 months) to the American propaganda by people like Dr Ralph Lapp and Lewis Strauss about a danger area of 7,000 square miles following the Bravo test of 1 March 1954. That was based on people remaining outdoors, with little clothing, and making no effort to decontaminate themselves or the area they are in for the entire period of exposure. As proved in earlier posts (for example here, here, here, etc.), a dose of 40 R at Hiroshima and Nagasaki was insufficient to even merely double the normal very small risk of leukemia, so if you did get leukemia after receiving 40 R in Hiroshima it was about 75% likely to be natural, not due to radiation (as proved in the previous post). With other forms of cancer (solid tumors), the increase in natural risk was even smaller than it was for leukemia.
Once people return after 3 months to an area at an outside dose rate of 0.3 R/hour, they can decontaminate it, by road sweepers to remove dust and water hosing to wash fallout off roofs into drains, where the gamma radiation is shielded from people, as explained in paragraph 11.26 of the 1959 Nuclear Weapons book, which is backed up by the 1959 Home Office Scientific Advisory Branch report CD/SA96, The decontamination of residential areas, which compiled nuclear test data tables on decontamination (from the USNRDL 1958 report Radiological Recovery of Fixed Military Installations, and other nuclear test fallout research reports). This gives decontamination effectiveness data for land and ocean burst fallout on different surfaces (deep plowing to reduce dose rates and the addition of potassium chloride to soil to block cesium-137 uptake by plants is used in agricultural areas). A further report in 1965, SA/PR-97, The value of area decontamination in reducing casualties from radioactive fallout, originally secret, planned even earlier decontamination by fire-hosing residential areas where the 1-hour reference gamma dose rate was 500-3,000 R/hr. The report finds that at levels of fallout below 500 R/hr at 1 hour, there are few casualties indoors in Protect and Survive handbook type "inner refuges" anyway (200 R producing a casualty), while higher levels than 3,000 R/hr at 1 hour tend to expose decontamination crews to excessive doses even 5 days after detonation, so evacuation is then a better option. The report shows that human-crewed decontamination work becomes feasible at 1-5 days after detonation, when the 1-hour outdoor dose rate of 500-3,000 R/hr has decayed to 10 R/hr. Decontamination crews restricted to areas below 10 R/hr cannot get more than 10 x 8 = 80 R in an 8 hour shift. (Obviously, modern technology would allow road sweeper/flusher trucks to be equipped with drone-type full remote control and cameras, reducing hazards.)
Therefore, the real fallout inconvenience encompasses an area less than the area of hazard from high velocity flying glass, even before you look at the reduced fallout doses from cleaner weapons with lead or tungsten fusion stage pushers in place of uranium-238, e.g. the comparisons of measured fallout in Operation Redwing weapon test report WT-1316 Table 2.11, showing that the maximum 48 hour land equivalent fallout dose downwind of 3,000 R outdoors (unshielded) covered an area of 520 square miles for 5 megaton 87% fission Tewa (a thermonuclear test at Bikini Atoll in 1956), compared to just 20 square miles for the clean bomb test, Navajo, which was just 5% fission but had a similar total yield of about 4.5 megatons (also at Bikini Atoll in 1956). Although Navajo was fired on a barge, the plot in Fig. 2.45 of the report using four different Redwing nuclear tests shows that the fallout areas only depended significantly on the fission yield, not the surface the bomb was exploded on or the wind.
Therefore, if anyone in politics has radiophobia, they can simply make our bombs cleaner (5% fission like Navajo, or 15% fission like Zuni, a 3.53 megaton test also fired in 1956). The enemy can be coerced into doing the same thing, because our protected second strike retaliation capability means that our deterrence doesn't require instant retaliation; we can wait to check if the apparent attack was just a meteor explosion, or a flock of birds on a radar, or a missile test by North Korea. Similarly, we can check the fallout to determine the bomb design and the fission yield, just as we did when Russia was testing in the atmosphere. If someone detonates a nuclear weapon which produces a lot of lingering contamination, we will take that into account in determining the reply. The 1961 Russian test of 50 megatons proves that was clean: we detected fission products from only 1.2 megatons after that test, proving a fission yield of 2.4%. Therefore, an enemy with a thermonuclear capability can potentially replace uranium-238 in the fusion stage with lead or tungsten, which have sufficient ablation density to compress the fusion fuel, without producing the large radiation doses you get from uranium-238 fission (neutron capture in an inert pusher contributes only trivially to the fallout hazard, as proved by Redwing weapon test reports WT-1316 and WT-1317).
If anti-clean nuclear weapons propaganda from politically biased people can be replaced with the truth, the experimentally proved facts of physics, then collateral damage can be averted even in a war, just as Hitler was discouraged from attacking England with kilotons of tabun nerve gas in V1s and V2s.
Another fallout controversy George R. Stanbury studied was the close-in fallout within the actual damaged area (reports CD/SA87 December 1957, classified Confidential, which we reviewed in detail here, and CD/SA94 which defends the upwind fallout predictions in the 1959 booklet) since that is precisely the area that civil defence search and rescue teams would need to work in. The close-in fallout around the crater was found to be much heavier in the 1952 Mike test where the bomb had a massive steel case (a total bomb mass of 82 tons, well beyond any airborne delivery system), which formed the basis for heavy upwind fallout dose rate predictions from megaton weapons in Glasstone 1957. However, when the upwind fallout data from the light aluminium-cased 1954 Castle and 1956 Redwing nuclear weapons trials was assessed, the upwind dose rates in the blast damaged area for similar fission yields and distances were found to be only 10% of those for Mike for land surface bursts and only 1% for ocean water surface bursts. The main downwind fallout pattern dose areas were similar for both types of burst, note however that the map scales for the Bikini Atoll for upwind fallout in reports WT-915 and DASA-1251 are incorrect for Operation Castle and exaggerate the fallout distances by up to a factor of two. Stanbury explains on page 44 of the 1959 Nuclear Weapons handbook, paragraph 8.27:
"The cloud model for the larger weapons indicates that very little fall-out is likely to be deposited upwind beyond the limit of complete destruction, unless the winds at all levels up to cloud height are of exceptionally low speed or are in opposite directions at different heights. ... The situation may vary from complete prevention of fire-fighting and rescue to complete freedom from fall-out in the damaged area beyond the range of complete destruction."
Stanbury in his Confidential December 1957 paper CD/SA87 uses two reports, Edward Schuert of the U.S. Naval Radiological Defense Laboratory in report USNRDL-TR-139 and also Dr Frank H. Shelton in an AFSWP report called Physical Aspects of Fall-Out which gives the in compressed form conclusions about local fallout based on dose rate meters, ocean surveys and rocket probing of the mushrooms for Operation Redwing, i.e. focussing on four thermonuclear weapons exploded at Bikini Atoll in 1956:
"We are forced, therefore, to conclude that the heavy upwind contamination for a wind speed of 15 miles per hour, which is deduced from Table 9.71 of Effects of Nuclear Weapons is incompatible with the presently accepted physical model of the explosion which explains the megaton trial data so well. For lower wind speeds, however, it is clear that contamination could extend further upwind; in the limiting case of still air some contamination could cover the whole area under the mushroom cloud ... Conversely, of course, higher winds would result in less upwind contamination; for example with a wind speed of 30 miles per hour it seems probable that only the largest particles (1000 microns) would fall upwind of ground zero and contamination would not extend outside the area of total destruction."
What is interesting here is that the land based measurements of fallout upwind from Redwing Tewa (5.01 Mt, 87% fission) covered most of Bikini Atoll and so are an extremely useful check on what Stanbury says. The simplistic idea of fallout particles drifting slowly downward would prevent any fallout at all upwind from the detonation in a moderate wind speed, because the mean in the particle size distribution is generally about 100 microns (0.1 mm) and most of the activity is located at the altitude of the base of the cloud, as proved by rockets with radiation meters and radio telemetry, fired through the Zuni, Cherokee and Tewa clouds in 1956. Therefore, even fallout beginning at the upwind cloud base would be expected to be blown downwind of ground zero, before being deposited. You would expect that any fallout which actually lands the upwind area would therefore consist of very large particles, several millimetres in diameter, like hail or heavy rain. However, this is not what was found by Peter Brown and others in weapon test report WT-1311, Gamma exposure rate versus time, Operation Redwing:
They found in Figure 3.18 that at 4.2 statute miles upwind from Tewa, although fallout started at just 15 minutes after detonation, the fallout took 3 hours to reach a peak of about 100 R/hr (after correction for instrument shielding protective factor of 1.4). Clearly, only small fallout particles would still be airborne at 3 hours after detonation, and you would expect that even moderate winds would have blown then downwind prior to being deposited. What seems to be the case is that, as Stanbury explains in the quotation above, with a large angular wind shear, winds blow in almost opposite directions at different altitudes, so the particles don't fall continuously in the overall downwind vector wind direction, but instead zig-zag upwind and downwind as the fall through successive wind layers. Therefore, some very small particles end up moving hardly any net downwind distance as they slowly fall through layers of opposing winds.
But there is another issue for close-in fallout, the downdraft around the toroidal vortex fireball as it rises:
In the 11 May 1959 issue of Life magazine, RAND Corporation fallout researchers Stanley Greenfield and Robert Rapp were pictured (photo above) modelling smoke rings against a blackboard, a piece of classical physics that goes back to the vortex atom theory of Lord Kelvin, who noticed that smoke rings showed stability and would bounce off each other when collided, so that in a perfect fluid which he called the ether (prior to Dr Einstein and the discovery of modern quantum field theory), fundamental particles would be indestructible spinning vortices. Air burst nuclear weapons in Nevada showed the toroidal vortex structure of rising fireballs clearly. Unfamiliarity with smoke rings has led to one 100 metres wide filmed earlier this year in Kazakhstan being falsely attributed to UFOs in a Daily Mail report. The explosion of large round buckets of smoke filled burning fibreglass resin in a factory in China last year produced perhaps the best example ever seen, as reported in the Daily Mail newspaper:
Robert Rapp's research on vortex fireballs is reported in two 1963 Secret-Formerly Restricted Data RAND Corporation reports:
RM-3605-DASA, On the behavior of large, hot bubbles in the atmosphere, and
RM-3788-DASA, Further progress toward a practical theory of nuclear cloud behavior.
Also: R. E. LeLevier, Cloud rise, RM-3822, RAND Corp., 1963, classified Secret-Restricted Data.
(For the basic physics, see Yoshimitsu Ogura's paper "Convection of isolated masses of a buoyant fluid: a numerical calculation", Journal of the atmospheric sciences, v19, 1962, pp. 492-502 or Alan Shapiro and Katherine Kanak, "Vortex Formation in Ellipsoidal Thermal Bubbles", ibid, v59, 2002, pp. 2253-2269.)
Rapp summarizes his results with extracts in his unclassified February 1966 RAND Corporation memorandum RM-4910-TAB, A re-examination of fallout models, which on page 5 explains:
"The buoyant forces come into play to accelerate the hot, low-density fireball upward. However, the fact that the pressure decreases with increasing elevation in the atmosphere results in an intersection of surfaces of constant density and constant pressure. According to Bjerknes's theorem for the creation of vorticity in an inhomogeneous atmosphere, this will cause the formation of the vortex ring that has been observed so frequently in the rising nuclear cloud. Thus, at this point, about 5 seconds after detonation, the fireball has been transformed into the nuclear cloud. All of the radioactive material is contained within this rising cloud. The outer, cooler edges of the fireball can contain no radioactive debris, because there has been no mechanism to transport it to the edge. After the vortex motion and buoyant rise has started, however, the fireball is essentially turned inside out."
Rapp then makes the important point that because the vortex is rising, the stream lines of flow within it are different depending on the frame of reference: if the cine camera is tilted upwards and follows the fireball while it rises, the stream lines of debris motion are perfectly centred around the radioactive ring, but films taken of the same fireball that do not follow it upwards effectively superimpose the motions within the spinning torus with the vertical fireball rise, creating the illusion that the torus of circulation has a larger radius than the glowing radioactive ring as Rapp illustrates in the comparison diagram below:
Rapp notes that "This account of the circulation has been verified by making accurate measurements of the edge of the visible cloud", citing H. G. Norment's Technical Operations Research report TO-B63-102, Final report: research on circulation in nuclear clouds. Allowing for 1 megaton cloud cooling by sucking in cool air and by adiabatic expansion as it rises, Rapp explains on pages 13-14:
"... it can be estimated that the average temperature of the rising mass falls to values close to those of the ambient atmosphere in about one minute. If there is some unmixed air from the fireball within the vortex core, that air would cool only at the adiabatic rate. Such a rate of cooling would reduce its temperature by only 60 % in 2.5 minutes. Thus, the temperature within the rising cloud at 2.5 minutes might range, for a 1 Mt device, from as low as 220 K to as a high as 2200 [citing as the reference for this, his secret report RM-3788-DASA, 1963]. ... Cooling by mixing and adiabatic processes destroys the cloud's buoyancy, friction destroys its circulation, and work against gravity destroys its vertical kinetic energy."
Above: Rapp computes a downdraft velocity of 626 miles per hour at a radius of 2.6 miles, 2.25 minutes after a megaton surface burst. As explained in American nuclear weapon test reports WT-4 and WT-615, this downdraft around the central updraft explains the existence of small particles in upwind fallout. Dust is sucked up by the central updraft, carried around the radioactive smoke ring, and is then blown downwards at the periphery. This explains why the gravitational settling rates contradict observed levels of fallout in the damaged area around ground zero, and explains some aspects of the fractionation of fission products. Radioactive gases like krypton-89 (which has a half life of 3.18 minutes) remain in the central hot smoke ring, which explains why their decay products (Rb-89 and Sr-89 in this example) are depleted from local fallout and concentrated in the distant fallout of very small particles.
On the other hand, metal oxides with high melting points like plutonium, uranium, Y-95, etc., condense into solid particles after just a few seconds and can get flung out of the rapidly rotating toroid by the centrifuge effect, where they are then able to collide with, and stick to, the surfaces of dust particles which have been sucked into the fireball by the central updraft. This centrifugal separation of particles from gases in the rapidly revolving toroidal cloud is why the fallout that lands near ground zero is enriched in refractory decay product chains like Zr-95, Nb-95, Mo-99, etc., and depleted in volatile isotopes of iodine, and strontium and cesium which have the gaseous precursors at early times, krypton-90 and xenon-137 (Dr Carl F. Miller explains this centrifugal fractionation mechanism in volume 1 of Fallout and Radiological Countermeasures, 1963).
Rapp explains on page 30 that for a 1962 Nevada test (Johnie Boy), 95 % of the strontium-89 was still in the cloud at 20 minutes after burst, whereas only 28% of the Zirconium-95 remained in the cloud. This is precisely because strontium-89 has the krypton-89 gaseous precursor in its decay chain, which keeps it in the vortex for several minutes while most of the fallout is being formed, whereas the precursor of zirconium-95 is a solid not a gas, so it gets thrown out of the vortex by the centrifuge effect and comes into contact with the desert dust, to form fallout:
"This analysis indicates that there is a great deal of separation of isotopes with particle size, refractory elements being concentrated in large particles and less refractory elements being concentrated in small particles."
Rapp points out that fallout samples collected near early Pacific H-bombs had a log-normal particle-size distribution used in RAND report RM-2148 (mean of 3.8 log microns, standard deviation of 0.69 log microns) that included some smaller particles, yet no where near the true abundance. This was because the samples landing near ground zero were biased in favor of larger particles (a skewed distribution, or statistical error). Rapp makes this error graphically crystal clear in his Figure 10:
This particle size fractionation effect was studied at British nuclear tests for civil defence purposes. For example, the ship harbour burst Operation Hurricane in 1952 gave highly soluble fission products in fallout containing sea water and black iron oxide produced in the fireball from the steel of the ship, whereas for bursts over silicate topsoil at Maralinga in 1956, the volatile fission product decay chains plated the outer surfaces of the particles, and were relatively more soluble than the metallic oxides which ended up trapped inside the melted particles. Table 27 in Dr John Loutit and Robert Scott-Russell's nuclear test fallout report AWRE-T57/58 shows that the water solubility of Buffalo-1 silicate soil fallout was 80% for strontium nuclides (-89, -90, etc.) and iodine nuclides (-131, -132, -133, -135), 40% for Ba/La-140, 35% for Te-132 and Mo-99, 5% for Zr/Nb-95, and only 3% for Ru/Rh-103. Thus, “fallout solubility” depends entirely upon the nuclide involved. It is therefore misleading to quote a percentage solubility figure without saying which nuclide is referred to. If you do quote an overall percentage for solubility, you have to say whether it is for beta or gamma radiaton and the time after burst, because the relative contribution of soluble nuclides varies with time. Plutonium oxides are almost entirely insoluble, whereas iodine is almost completely soluble because they are on the outside of the glassy particles.
AWRE-T57/58 shows that a total of 15% of the Buffalo-2 fallout was retained by pasture grass, mainly in the stem base. Table 15 in the report shows that threshing wheat after Buffalo-2 left 90% of the fallout on the husk of wheat and only 10% remains on grain after threshing, and the authors spell out the implications:
“At a dose rate of 50 R/hr at 1 hour, 80 kg of flour would contain only 0.06 microcurie of Strontium-90. ... The hazards arising from the consumption of contaminated flour appear therefore to be smaller by a factor of more than a thousand than those arising from milk.”
The Buffalo-2 result that only 10% of fallout gets through through the threshing process to contaminate the flour is stated in paragraph 10.16 of the 1974 edition of Nuclear Weapons, but AWRE-T57/58 is not cited and there is no indication provided that this fact comes from an actual nuclear explosion experiment, done at great cost. Consequently, the data does not appear impressive to readers, who are left unaware of whether the facts are guesswork or actual evidence. This is a fatal situation for such a controversial subject.
Likewise paragraph 10.20 points out simple well proven countermeasures to the iodine threat. Limiting fallout contaminated milk consumption for a month after a nuclear explosion is an adequate countermeasure for ingested fallout, while the iodine-131 decays. Contaminated milk need not be wasted: it can be frozen, powdered, or processed into cheese or ice-cream that can be stored for a month while iodine-131 decays with its 8 days half-life, during storage. Alternatively, cattle can be kept in barns on winter fodder while the iodine-131 decays on fields outdoors. Temperature has no effect on radioactive decay, so it is safe to freeze radioactive fallout contaminated food while it undergoes rapid radioactive decay. Fallout uptake by the roots is relatively small and was well investigated in American nuclear tests.
Robert Scott Russell of the Agricultural Research Council, Radiobiological Laboratory, England, after analyzing the nuclear fallout in Maralinga wrote an interesting paper called "The Extent and Consequences of the Uptake by Plants of Radioactive Nuclides" which was published in the Annual Review of Plant Physiology, volume 14 (June 1963), pages 271-294:
“Iodine-131 is ... of concern primarily as a source of exposure of infants who consume appreciable quantities of fresh milk, partly because of the very small size of their thyroid glands in which it is concentrated, and partly because milk is usually the most highly contaminated food. Doses to infants from iodine-131 have on occasions been considerably higher than those from any other component of fallout; for example, towards the end of 1961 it was estimated from the analysis of milk that the thyroid glands of infants fed on fresh milk in the United Kingdom would have received about 170 mrems. ...
"Caesium-137 which was deposited on foliage of plants appears to be retained relatively similarly to strontium 90, and like strontium it is readily removed from foliage by rain. The concentration of caesium-137 within different tissues which results from direct contamination, however, can contrast very markedly with that caused by strontium-90. This is due to the mobility of caesium-137 within tissues; thus nearly 30% of the caesium-137 which has been deposited on the foliage of potatoes may reach the tubers, as compared with less than 1% of strontium-89 ...
"Plutonium. Because of its very long half life and high toxicity to animals consideration has been given to the entry into plants of the fissile element plutonium. A very slow rate of absorption is to be expected because it forms high valency (usually 4 or 6) ions; this has been confirmed in several studies and, over 1.5 years, grass grown in pot culture may absorb less than 0.0001% of that added to the soil.”
For these reasons, root uptake is not a problem as long as there is enough potassium in the soil to saturate it and deter cesium-137 uptake (potassium chloride can be added to the soil if not). Growing potatoes minimises strontium-90 uptake. In any case, because of fractionation, iodine, cesium and strontium are reduced in local fallout, which is enriched in insoluble nuclides which are not a root uptake problem, such as plutonium. The water soluble root uptake nuclides concentrate in the tiny particles of global fallout, so that problem is dispersed around the world like the 170 megatons of atmospheric nuclear test fallout, which was well studied: even iodine-131 to kids thyroids proved to be insignificant, compared to the large doses needed to significantly boost the natural incidence of thyroid cancer.
Scott Russell explained in his paper in the massive 1970 symposium, Survival of food crops and livestock in the event of nuclear war there is no significant problem from root uptake in a nuclear war. Even if a thunderstorm causes heavy rainout, the heavy rainfall helps to decontaminate it, by washing it either deep into the soil where it is shielded, or into storm drains, where it is again shielded. It has proved trivial compared to the external gamma ray dose soon after detonation! For this reason, the 1974 Nuclear Weapons book shows how to decontaminate food by washing or peeling the layer with fallout off or discarding pea pods and the outer leaves of cabbage.
Moving on the radiation dose calculations, the Home Office Scientific Advisory Branch report CD/SA45, Gamma radiation dose rates at heights of 3-3000 feet above a uniformly contaminated area, incorporated scattered gamma rays into the Samuel Cohen's RAND Corporation calculations of the dose rates above contaminated areas, which had been published as an appendix to Glasstone's 1950 Effects of Atomic Weapons. This is also the origin of the British calculating scheme for protective factors of buildings. On a flat plane, about 90% of the 0.7 MeV gamma dose at 3 feet height comes from direct gamma rays from the ground and since the gamma rays have a long range, most of this radiation is coming almost horizontally, while 10% is air scattered and is thus coming from many directions in the sky. The radiation dose in a building can therefore be calculated utilizing this geometry, making suitable allowances for roof contamination which depends on the roof angle and rainfall (CD/SA 103) and fallout ingress. These factors are in most cases less important than the assumption used about the gamma ray energy. Dr Triffet disclosed at the June 1959 congressional nuclear war hearings that for close-in land burst thermonuclear fallout, the gamma ray energy during the sheltering period for a week or two after burst drops to just 0.25 MeV due to Np239 and U237 formed in the U238 jacket.
This means that during the main sheltering period, any building offers far more protection against fallout than predicted using the usual assumption of 0.7 MeV from Glasstone, 1 MeV for calculations using the 1 hour energy, or 1.25 MeV for experiments using cobalt-60 sources (which emit two gamma rays, 1.17 and 1.33 MeV, giving an average of 1.25 MeV). Stanbury like Triffet predicted large contributions to fallout radiation during the sheltering period from low energy Np239 using British nuclear weapon trial Operation Totem and Hurricane neutron capture data, in his 1959 report R and M 75. Ignoring this low energy of the gamma rays offsets the errors of ignoring fallout ingress effects. What percentage of rainfall normally enters a house? If the windows are open, some will on the side facing the wind, landing on the window sill and maybe the floor nearby. However, while sheltering, people can use a damp cloth or mop to clean up and throw out any dust that enters. There are cleaning devices in every house to decontaminate fallout: dust cloths, paper towels, vacuum cleaners, brushes, etc. The idea that people are going to stay indoors for two weeks of sheltering without finding the time to clean up any fallout ingress is clearly the usual biased scare-mongering of political anti-nuclear fanatics.
John Newman examined effects of fallout blown into a buildings, due to blast-broken windows, in Health Physics, vol. 13 (1967), p. 991: ‘In a particular example of a seven-storey building, the internal contamination on each floor is estimated to be 2.5% of that on the roof. This contamination, if spread uniformly over the floor, reduces the protection factor on the fifth floor from 28 to 18 and in the unexposed, uncontaminated basement from 420 to 200.’
But measured volcanic ash ingress, measured as the ratio of mass per unit area indoors to that on the roof, was under 0.6% even with the windows open and an 11-22 km/hour wind speed (U.S. Naval Radiological Defense Laboratory report USNRDL-TR-953, 1965). So Newman's 2.5% assumption is a severe exaggeration of the ingress problem.
A problem occurs for the cobalt-60 bomb, popularized by Stanley Kubrick's film and many books and papers, starting with Leo Szilard in 1950 during his fanatical anti-H-bomb campaign. (Szilard couldn't imagine a U238 jacket, which is effective, only an ineffective Co-60 jacket.) Cobalt-60 was included in an Operation Antler test in 1957, resulting in the Co-60 remaining only in large metallic pellets, millimetres in diameter, which landed in the vicinity of ground zero. This is because cobalt has no gaseous precursors, so it is highly refractory and lands in large particles near ground zero. Little ends up in global fallout, which is depleted in refractory nuclides and enriched in volatiles. In any case, the long half life (over 5 years) results in very low specific activity. As explained, Co-60 emits two gamma rays totalling 2.5 MeV for every neutron captured in cobalt-59; using the same neutron to split U238 gives 200 MeV, i.e. 80 times more energy, including far more residual radioactivity, some of which is volatile nuclides which does get into global fallout. Finally, even if someone was to set off a massive Co-60 bomb as the film On the beach imagines, the slow build up of the radiation gives plenty of time to decontaminate it before receiving an significant dose (the same applies to nuclear reactor fallout). Scare-mongering relies on trying to divert attention from genuine countermeasures and physical understanding, towards political activism like banners, shouting, hate attacks, marches, and a fear based culture. Nuclear physics is being made part of old horror film culture.
Debunking of fire storm and thermal burns exaggerations, due to thermal radiation shielding
In Hiroshima and Nagasaki, air scattered thermal radiation did not prove effective in causing burns or starting fires: only skin or dry kindling exposed with a direct view of the fireball (no intervening trees, people, or buildings) were burned or ignited. George R. Stanbury investigated this thermal shadowing effect in detail for British cities, as we documented in previous posts. The 1959 edition of Nuclear Weapons states the conclusions on page 28:
"In a built-up area ... even from a high air burst the buildings would have a considerable shielding effect on one another [once the distance from ground zero is several times the optimum burst height, the thermal rays are coming almost horizontally and will be intercepted and stopped by the first buildings they arrive at]. ... A firestorm only occurred ... where at least every other building [50% of buildings] in the area has been set alight by incendiary attack. ... studies have shown that a much smaller proportion of buildings than this would be exposed to heat flash (due to shielding). Moreover, the vulnerable centres of many British cities were destroyed in the last war and the new buildings which are replacing them are mainly of fire-resistant construction and less closely spaced."
The British WWII improvised shelters against fire (incendiary bomb effects), blast and gas effects were applied to nuclear weapons survival after verification by nuclear test experiments. Similarly, the Swiss Federal Authority's Office of Civil Defense applied similar techniques for sealing up doors and windows against blast, heat and fallout to those used in WWII refuge rooms in buildings and in Cold War nuclear civil defense, in their 1977 handbook, Technische Anleitung für die Herrichtung von Behelfs schutzräumen (TA BSR 1977), which translates as Technical Instructions for the fitting-out of makeshift shelters:
Update (1 July 2015)
Resolving a problem with Longmire's high altitude burst early time EMP prediction formula
"In fact, I basically designed the first boosted bomb device. ... I got interested in what's called nuclear effects, the effects of nuclear explosions. In fact, I really got interested in that in 1962 when we had the high altitude test series, Operation Dominic. And I started working in that, and it turned out that the AEC, or Los Alamos Laboratory, was not really very interested in the effects of nuclear explosions by that time. In the early days, they had done a lot of good work on blast and shock and fallout and that kind of stuff. But by that time, most of the people there regarded their main job as putting bombs in the stockpile, and there wasn't too much appreciation that it was important to understand about the physics of nuclear effects, for example, EMP. ... way back in the 1970s, early seventies, there was a fellow at the RAND Corporation, this is after the RDA physics group [Harold Brode et al] left. His name was Cullen Crane [see illustration below], who, I don't know if you've ever heard of him—well, anyway, this fellow was saying that EMP is a hoax. These guys are either crazy or they're doing it to, you know, perpetuate their salaries. And so the Jason group got tasked by DNA to look into this. Now, in this case, in my opinion, the Jason group didn't do a very good job, because instead of reading the reports and trying to settle the argument, they started out from scratch and first did their own version of EMP, and at least, I didn't think that was necessary at the time. ... They do not, you know, when they begin to look into something, they don't go back and make sure that they've read all the earlier references and stuff like that. But you don't expect physicists to be your formally good historians."
- Dr Conrad Longmire, interview given to American Institute of Physics's Finn Aaserud, 30 April 1987.
The attack quoted above by Longmire on RAND Corporation Cullen M. Crain's alternative method of calculating EMP, by summing individual electron EMP emissions rather than solving Maxwell's equations, seems a bit over the top. Yet that is the standard, very paranoid, response which often greets alternative theories in physics. Crain's unclassified version of the 1973 paper, his 1982 Calculation of Radiated Signals from High-Altitude Nuclear Detonations by Use of a Three-Dimensional Distribution of Compton Electrons (DTIC ADA114738 or RAND N1845) gives results that agree with other more standard techniques in the applicable cases. There is a tendency to be extremely defensive about the first theory to arrive on the scene, to the point of trying to use it to close down efforts to work on alternatives! If you have an alternative idea, you first try the polite method, but you get brushed off rudely, like a fly. Then you give them a taste of their own medicine, and they have the temerity to call you rude! This is a pretty standard problem. Whatever approach you take, some contrived, specious excuse is used to silence it.
High altitude EMP data is compiled in an earlier post, linked here. The January 2014 issue of DTRIAC Dispatch discussed late-time EMP, which is extremely low frequency (ELF) and therefore penetrates some metres into dry ground, where it couples to very long cables. What's generally more dangerous is the early time or E1 phase of the EMP which delivers frequencies up to 100 MHz, in the UHF spectrum, with intensities of up to 50 kV/m for a fraction of a microsecond. The problem is that although EMP effects from a 1.4 megaton burst at 400 km (Starfish) in 1962 are well known, the correct scaling laws for the terrorist threat from say North Korea detonating 7 kt (the yield of its last nuclear test) at say 100 km altitude, are not openly discussed. EMP Theoretical Notes are now online, and they document the early-time EMP research by people like Conrad Longmire of Los Alamos, who is credited with being the first to understand the Starfish EMP from 1962, where the earth's magnetic field deflected Compton electrons, producing an EMP. (Glasstone discusses EMP in the April 1962 edition of The Effects of Nuclear Weapons, but not that mechanism.) Longmire's EMP mechanism was first published openly by RAND Corporation's Karzas and Latter, report RM-4306 (DTIC document AD607788), crediting him.
The only published paper giving plots of early EMP peak field strength versus yield (of prompt gamma rays escaping from the weapon) and burst height is the Master's Thesis of Louis W. Seiler, Jr. His plots show a generally very weak and complex dependence of yield and burst height on the EMP. The problem with numerically integrating differential equations with a computer is the lack of understanding that results. This problem also plagues weapons design and other nuclear effects computer codes. Hence, there is a need to try to come up with analytical solutions. Naively, you might take the equation for electromagnetic wave energy density in terms of field strength (energy per unit volume is half the product of the permittivity of free space, and the square of the electric field strength), and give the EMP a volume equal to the that of the prompt gamma ray pulse (a 10 ns pulse for instance is a shell 3 metres thick, since the gamma rays and EMP are going at light velocity which moves 3 m in 10 ns). This gives a simple formula where EMP field strengths are proportional to the square root of the yield, divided by the distance from the bomb. This naive theory is completely misleading, largely because the Compton current is largely cancelled out by an opposing conduction current, at least for small distances (between bomb and atmosphere), and large yields. (In addition, you need to take account of how far the Compton electrons travel before absorption in the air at the altitude in question, in comparison to the their gyro radius in the geomagnetic field.) However, Karzas and Latter found an analytical solution to this conduction current limitation of the EMP in their equation 52 (the symbol sigma is the air conductivity, signifying the conduction current term in equations 51 and 52):
I've highlighted the two key parts in red. The first is ellipse covers the Compton current contribution, basically the Compton current density j integrated over a radial line through the deposition region, with the EMP also inversely proportional to distance. The second term, multiplying the first, is a exponential attenuation factor for the effect of the conduction current. In fact, this general analytical solution to the EMP first appears in equation 12 of another RAND Corporation paper on EMP issued more than a year earlier, W. Sollfrey’s RAND Corporation report RM-3744-PR, An Analytically Solvable Model for the Electromagnetic Fields Produced by Nuclear Explosions, July 1963, EMP Theoretical Note TN53. This analytical solution was generally ignored or solved numerically, and was not simplified into a simple model for EMP field strength calculations. Our argument is that it can be simplified with good approximations (such as taking the air conductivity to be constant through out the gamma ray deposition region "pancake" under the burst), to give a simple model to explain Seiler's curves. Moving ahead to 1987, Longmire and others reinvent the wheel (in separate parts!) in equations 9 and 10 of EMP Theoretical note 354:
Longmire's 1987 EMP theoretical note in a way helps by breaking the product into two parts that can be multiplied together. Each part, Compton contribution and conduction current, lead to questions and answers that are very important. First, EMP like radio is the time-derivative of the net current, not its integral (the opposite of taking a derivative!), so how can you get a correct result from equation 9?
The answer to this is profound for Maxwell's theory of electromagnetism, for it means that Longmire's EMP, radiated due to the sideways deflection of Compton electrons travelling at nine-tenths of velocity of light, is showing us how radiation really occurs, in all cases. There's a duality between Gauss's law of static charge (the radial electric field) and electromagnetic radiation due to charge acceleration. In other, plainer, words: when the Compton electrons are deflected sideways, part of their radial field (modelled conventionally by Gauss's law!) is converted into synchrotron radiation. Conventionally, Maxwell's equations say that the radiation from an oscillating charge is not the Gauss field (see for example, equation 28.3 of the Feynman Lectures on Physics, volume 1, where separate terms are given for fields due to charge acceleration and static charge).
Take mass and energy. They were once considered completely different. Then it was discovered that under certain conditions, significant conversions between them could occur (e.g. in fission and fusion). By analogy, the validity of Longmire's result means that the Gauss field and electromagnetic radiation are the same thing in certain conditions. What we're pointing out here is that if you have an electron moving at 0.9c and deflect it sideways by a magnetic field, the Longmire equations prove that some of its c-velocity Gauss field is being sheared off, and is continuing along its original path without deflection. That's the mechanism of electromagnetic radiation by accelerating charge.
The lost field energy from the electron then appears as a deceleration of the electron (loss of kinetic energy). This is proved by the very fact that Longmire's proof-tested equation must be a duality to Maxwellian synchrotron radiation. In quantum field theory, the Gauss field isn't static at all but is composed of light velocity exchange radiation, virtual photons (electromagnetic gauge bosons). So this really makes the case for understanding the Maxwell equations in terms of moving virtual photons; it's obvious that these virtual photons become real photons (observable radio waves or EMP, for instance) when the charge is accelerated, breaking the normal equilibrium of exchange of virtual photons between charges, which constitutes the field extending throughout space.
Secondly, this analytical solution provides easy predictions of EMP, explaining Seiler's graphs. Here are the first couple of pages from my draft paper on this topic, which are needed here because the symbols are hard to typeset neatly in a blog's font:
 |
| 1974 edition of the "Nuclear Weapons" civil defence handbook (compare it to the original 1956 edition, post Operation Hurricane, but pre-Operation Buffalo, linked here): based on secret nuclear test data (particularly work done by George R. Stanbury and Frank H. Pavry at Operations Hurricane and by AWRE's Dr Loutit and Dr Scott Russell on fallout from the Buffalo-2 surface burst in Australia), it covered up its detailed research basis and was easily "ridiculed" (despite being well founded on fact) by CND's Phil Boswell in "Civil Defence: the Cruellest Confidence Trick". |
 |
| Firestorms in modern cities debunked 1964 |
This post will correlate the originally secret (now declassified) UK National Archives reports upon which the book was based with the specific facts given on civil defence countermeasures.
Nuclear Weapons had three editions during the cold war (1956, 1959 and 1974). The first edition is the best organized as we previously discussed, with the 1959 and 1974 editions being obfuscated by a more complex, broken-up structure of chapters (e.g., fallout radiation information is dispersed in a disorganized manner between chapters 1, 2, 3, 8, 9, 10 and 11, with other effects like initial radiation, blast, cratering, and thermal in chapters 4-7). The original 1956 edition is more straightforward, with all the fallout radiation well organized and better illustrated in chapter 3 (the 1956 illustrations of the protection factors against fallout in buildings of different sizes and in different kinds of trench shelters were removed from the 1959 and 1974 editions). In addition, while chapters 1-10 have the same titles in the 1959 and 1974 editions, the final chapter in the 1959 edition, Chapter 11: Summary of Methods of Protection and Decontamination for the Individual, was removed in its entirety from the 1974 edition; that 1959 edition chapter showed on page 59 that to avoid ignition of bedspreads and curtains, they can be made fireproof with a fire-retardant solution (which allows fabric to smoke when exposed to an intense thermal pulse, without allowing sustained ignition once the thermal pulse ends):
"Suitable solutions for household use are 3 lb boric acid plus 2 lb sodium phosphate (or, alternatively, 3 lb borax plus 2 lb boric acid) dissolved in 3.5 gallons of water. Curtains and fabrics should be thoroughly soaked in the solution and the excess liquid squeezed out before they are rinsed and dried."
It also states on page 61:
"Curtains or sheets should be tacked over broken windows to keep gross amounts of fallout from being blown into the rooms. ... If dust was visible later in any room, it should be swept and dumped outside."
It explains that sustained skin contact with fallout causes delayed beta burns on page 62, adding:
"Contaminated clothing can be cleaned to a very considerable extent (almost complete removal of fallout particles)" by "an efficient vacuum cleaner" or "5 minutes in a washing machine or 5 minutes vigorous stirring" in water. This was proved by clothing decontamination trials at British land detonation tests and at the Nevada nuclear tests of Operation Jangle in 1951, as reported in weapon test report WT-347. The low contamination risk for clothing in a land burst nuclear explosion was proved at those tests in 1951:
"Four hours after the surface detonation, eight teams of men worked for a period of one hour in the contaminated areas. Five days after the underground detonation, one team walked and one team walked and crawled through the 10 to 500 milliroentgen per hour area, downwind from Ground Zero. The walking team traveled approximately 1/2 mile in 1/2 hour. The walking and crawling team crawled ten yards in the 300 milliroentgen per hour zone. ... Of protective clothing worn by men after the surface detonation, gloves and boots worn into areas near Ground Zero were the most highly contaminated, giving readings ranging from .01 to 9 mr/hr at six inches when monitored 26 hours after the detonation. Contamination of underclothing was negligible. Of the clothing worn into the contaminated area produced by the underground detonation, the maximum reading was 3.7 mr/hr. The men who crawled received only 2 to 4 mr from their clothing while receiving a total dosage of 1 to 2 roentgens, as measured by film badges which recorded radiation from both the clothing and the ground ... the level of radiation due to dust on clothing throughout the tests was negligible." - nuclear weapons test report WT-401, 1952.
The deletion of this final chapter on defence from the 1974 edition was a mistake. Exactly the same thing occurred with the American manual by Glasstone and Dolan, The Effects of Nuclear Weapons, Chapter 12 Principles of Protection which had been in the 1957 and 1962/4 editions was removed in its entirety from the final 1977 edition. This marked a complete change from Glasstone's stated objective on page 1 of the 1950 edition, titled The Effects of Atomic Weapons, which was making the case publically for civil defence.
If you present information on effects of nuclear weapons for a range of yields, CND inspired prejudice ensures that the public will look only at the effects of the highest yield given, 10-20 megatons, and then exaggerate the problem as a means to avoid confronting the facts realistically. By analogy, when seatbelts were introduced, people who did not want to wear them argued that they would produce a false sense of security and encourage people to drive faster, and would be hinder escape if the petrol tank exploded. The lesson is that it is necessary to focus on the most probable dangers, and to reduce them, instead of inventing spurious arguments that do not apply in the majority of cases.
The popular anti-nuclear propaganda works by a focus on large megaton yields which won't fit into missiles. A one megaton yield requires nearly a ton of bulky warhead if the weapons are cost effective, and that won't fit in the Trident SLBM, and only one such weapon can fit in a Minuteman class ICBM. Even the colossal and now obsolete American Titan II missile, big enough to put a small satellite into orbit, could only launch a single nine megaton warhead. In reality, the majority of warheads are submegaton. (As the tragic fate of MH17 proved last year, Russian cold war BUK ground-to-air missiles can shoot down aircraft carrying larger bombs.) The point is, anti-nuclear biased propaganda has gone so far into lunacy that only the least probable, largest yield nuclear weapon, is considered in an effort to debunk civil defence by populist scare mongering. Most physicists are still duped into the delusion that, to use an analogy, home fire insurance is no use because if your house catches fire, you and your family will be overkilled by invisible carbon monoxide gas, hot dust fumes, radiant heat, convective flame heat, and even if you and your family survive, you will be horribly mutated by terrible burns, brain and lung damage by fumes, etc.
Moving back to the nuclear bomb, the Trident and ICBM protected second strike capability is an anti-accident countermeasure, removing the necessity to escalate in case of accidents or mis-judgements, and removing the need to "launch on warning" (which was actually the "fail-safe" threat of Stanley Kubrick's anti-nuclear propaganda film). So, as with Hitler's non-use of 12,000 tons of tabun nerve gas in WWII, even if war breaks out with another nuclear power, we can continue to deter escalations to full-scale strategic nuclear attacks by the threat of the protected second-strike capability, just as our gas masks, mustard gas stockpile and proof-tested anthrax cattle cakes in WWII helped to deter Hitler's use of WMDs like tabun and sarin nerve gas (which he could have loaded into the V1 cruise missiles and V2 rockets). What about improvised terrorist nuclear weapons and accidental (primary stage or one-point) bomb explosions? The existence of a protected second-strike capability is a deliberate and successful de-escalator of accidents, a technique to prevent escalation. As a result, the most likely nuclear explosions are low yield terrorist attacks.
Even "accidental nuclear explosions" (bombs dropped by accident) are far more likely to go off with a relatively low yield than at their maximum yield, due to safety measures such as one-point implosion safety which ensures that in an accident the nuclear yield is trivial in comparison to the conventional explosive yield, which itself is impact and fire resistant, requiring a special type of explosive detonator to set it off (in addition, the capacitor charging, neutron initiator tube timing, tritium boost gas release into the core, etc. must all occur before it is even possible for a firing switch to "accidentally" set off a full yield explosion in an impact, contrary to ignorant annotations on a declassified document quoted by Eric Schlosser's Command and controlC book). Tests of deliberately burned nuclear weapons proved that there is no significant hazard. Nobody in the media panicked when a huge dose of polonium-210 contaminated a trail around London in 2006 after being placed into the tea of Mr Litvinenko by alleged agents of Mr Putin, a dose which was so massive that it caused not merely increased long-term cancer risks but actual short-term radiation damage resulting in organ failure.
The newspapers and TV did not run scare stories about the (small) risks from spilled tea on tables, sweat and exhaled air from someone contaminated, and so on. Nor do they do so when alpha emitter Am-210 is burned in household smoke detector fires. The reason of course is that there is no profit from scare-mongering in these cases. Mr Joe Public can see that whatever the risk, there's also a very real risk of being run over by a taxi or bus, hit by a cyclist, mugged, or being exposed to pollution in London. If a smaller hazard existed from a burning nuclear weapon in an accident, the story would be very different, because many people have been duped or brainwashed by one-sided propaganda into the notion that giving up nuclear knowledge and going back to the conventional weapons era of world wars, is a good cause.
Polonium-210 incidentally is used with beryllium as a neutron initiator for primitive nuclear weapons like the 1945 designs, so the very fact it was available in lethal quantities in London in 2006 after being smuggled in without detection goes to prove that the triggering of a smuggled nuclear weapon is not beyond the realms of possibility. The people who smuggled Russian polonium-210 into London to commit murder of a Russian dissident are hardly likely to be the kind of people you would trust. They might as well as sold it to terrorists.
The origins of British blast effects research for nuclear weapons
The very first assessments of air blast from nuclear weapons were done in London in 1941, during World War II, long before Los Alamos was set up in New Mexico, by physicists Penney and Taylor at the Civil Defence Research Committee (RC) of the Ministry of Home Security, London (wartime version of the Home Office, with responsibility for civil defence). Examples of these reports are RC-210 from early 1941, Sir G. I. Taylor's The Formation of a Blast Wave by a Very Intense Explosion (which was published in 1950, see link here with an extra portion comparing the prediction to the Trinity blast data) and Lord William G. Penney's October 1941 RC-260, On the Development of Suction behind a Blast Wave in Air, and the Energy Dissipation, and his co-authored December 1941 RC-286, Note on the Rate of Dissipation of the Energy of the Blast Wave.
"... the radii of ... damage ... for ground burst bombs would be increased possibly by as much as 30 % if the weapon were air burst at about the optimum height." - Nuclear Weapons, 1959, paga 7.11, p33.
This claim is well founded (see British versus American nuclear test data curves below) but as the British Medical Association and anti-nuclear group SANA (Scientists Against Nuclear Arms) publicised in 1983, it conflicts with the American data showing an increase by up to 50% in blast damage ranges for a few psi. However, page 6, para 1.22 in the same book makes it clear that the optimum blast damage height of burst is 1,000 ft for a 20 kt air burst (well above the fireball radius, thus averting intense fallout), which by the cube-root scaling law is equivalent to a 1 kt air burst at 368 feet, which as the graph below shows, optimises very high overpressures, and only causes about a 30% increase over ground burst radii for low pressures. Where the BMA and SANA go wrong is in their unstated but evident prejudice that capitalist America is always right and imperialist Britain is always wrong, in any dispute:
Above: British blast wave nuclear test data from William G. Penney, compared to Glasstone and Dolan, Effects of Nuclear Weapons (i.e. the unclassified summary of data in the secret report series DASA-1200). Penney published a summary of the British height of burst curves in 1970 in his 68 pages long analysis of the nuclear destruction of modern buildings in Hiroshima and Nagasaki (using British nuclear test data to determine the shielding effect of blast energy by damage to buildings), but the original data report by AWRE remains classified and retained from public display in the UK National Archives (reference ES 12/19, Comparison of British air blast with nuclear weapons blast phenomena: Part 3; variation of air blast on the ground with height of burst; AWRE Foulness, report AWRE/DASA/1200/3, Retained by Department under Section 3.4; Retained in departments on security or other specified grounds).
Blast wave attenuation by damage done in a modern city: hard facts from actual experimentation
The blast attenuation curve for Hiroshima is the effect of buildings absorbing blast wave energy. In a city, the blast wave is attenuated rapidly due to the buildings, contrary to Glasstone's data for blast over unobstructed desert; an effect proved by Penney in his comparison of blast over concrete, dark desert sand, and the cities of Hiroshima and Nagasaki. Energy must always be conserved, but this is traditionally ignored by the American manuals on the capabilities of nuclear war. Energy is removed from the blast wave by the following four fundamental processes in a city:
1. SEISMIC WAVES WITHIN THE BUILDING MATERIAL. Some of the blast energy is transformed into a seismic wave in the concrete or steel of the building material, similar to a ground shock wave. This is however only a relatively small use of blast energy. (Traditionally, a "no-go theorem" is invented by dogmatic, politically biased groupthink, whereby you ignore all sources of blast energy loss due to buildings by just calculating the trivial energy loss caused by sending a shock wave into a building frame, prove it to be trivial, then "close down the argument" about blast energy loss, while always ignoring the mechanisms that absorb most of the blast energy! This kind of "reductionist fallacy" occurs everywhere.)
2. DAMAGE TO BUILDING. Breaking the thick large glass windows and wall panels of modern city buildings absorbs some blast wave energy (quite apart from the seismic coupling mentioned above). This energy is used in breaking the chemical bonds in the materials, like the crystalline lattice of the glass. This energy ends up as a small rise in temperature of the debris.
3. KINETIC ENERGY OF DEBRIS ACCELERATED BY THE BLAST WINDS. Once windows are broken, the winds behind the blast front accelerate the fragments to some extent. The peak wind velocity behind a 1 psi peak overpressure blast wave is 40 miles per hour, but the blast wave has passed at supersonic velocity before the debris has been accelerated to 40 mph. Nevertheless, this can be very important in absorbing the energy of the drag or dynamic pressure of the blast wave. (Blast walls, for instance, work by deflecting and stopping the blast winds. If a building wall survives the blast wave, it does the same job of stopping the blast winds/dynamic pressure and has a shielding effect.).
The first discussion of blast energy depletion due to cumulative energy use (physical work done, E = Fx) to buildings in a city is in Hans A. Bethe's 13 August 1947 Los Alamos report LA-1021, Volume VII, Blast Wave, Part II, Chapters 5 through 10, which contains Chapter 10 by John von Neumann and Fredrick Reines, The Mach Effect and the Height of Burst, section 10.1 General Considerations on the Production of Blast Damage (pages X-1 to X-2):
"As to the detailed description of the target ... the structures ... have the additional complicating factor of not being rigid. This means that they do not merely deflect the blast wave without absorbing energy from it, but take a tariff on the blast at each reflection.
"In addition to be weakened by destroying structures, the blast wave may, of course, also be weakened by imparting kinetic energy to the debris. The removal of energy from the blast as it does its job decreases the blast pressure at any given distance from the point of detonation to a value somewhat below that which it would have in the absence of dissipative objects ... The presence of such dissipation makes it necessary to consider somewhat higher values of the pressure than would be required if there were only one structure set by itself on a rigid plane."
"... the structures ... have the additional complicating property of not being rigid. This means that they do not merely deflect the shock wave, but they also absorb energy from it at each reflection.
"The removal of energy from the blast in this manner decreases the shock pressure at any given distance from the point of detonation to a value somewhat below that which it would have been in the absence of dissipative objects, such as buildings."
This was removed from future editions, and replaced by a false claim (defying the conservation of energy) that blast waves effects can be increased in cities by reflection! Actually, the reflection process that enhances peak overpressure does not violate conservation of energy in the blast wave: the mechanism for the increased overpressure upon reflection by a rigid surface is simply that: (a) while the blast rebounds, it temporarily travels through itself, temporarily doubling the peak overpressure (this effect ceases when the blast wave has moved away from the surface, and is restored to the normal pressure) and (b) the stopping of the dynamic (wind) pressure by a rigid, perfectly reflecting wall simply converts the dynamic pressure into overpressure, so you are not getting something for nothing, you're just changing one thing (dynamic pressure) into another thing (overpressure).
Since both overpressure and dynamic pressure contribute to blast effects, it is simply not automatically true that blast reflection enhances the net blast effect: it enhances overpressure near the reflecting surface, but at the expense of the dynamic pressure. If you get a massive reflection factor due to such reflection, some of the energy diffracts upward as the blast moves over the structure, and it doesn't all diffract back down on the opposite side after passing over. Some energy is always lost. If you shout in a built up area, the sound is attenuated faster than over unobstructed ground, despite the diffraction of some of the sound waves around structures. Diffraction is not 100% energy efficient, due to both energy losses upward to the sky and to absorption of energy by structures. This isn't "speculative guesswork": it's down to the conservation of energy, one of the strongest empirical facts of nature.
Professor Bridgman (Introduction to the Physics of Nuclear Weapons Effects, DTRA, 2001) considers a building with an exposed area of 163 square metres, a mass of 455 tons and natural frequency of 5 oscillations per second, and finds that a peak overpressure of 10 psi (69 kPa) and peak dynamic pressure of 2.2 psi (15 kPa) at 4.36 km ground range from a 1 Mt air burst detonated at 2.29 km altitude, with overpressure and dynamic pressure positive durations of 2.6 and 3.6 seconds, respectively, produces a peak deflection of 19 cm in the building about 0.6 second after shock arrival. The peak deflection is computed from Bridgman's formula on p. 304: deflection at time t is given by: xt = [A/(fM)] {integration symbol} [sin(f t)] (Pt + CDqt) dt metres, where A is the cross-sectional face-on area of the building facing to the blast (e.g., 163 square metres), f is the natural frequency of oscillation of the building (e.g., 5 Hz), M is the mass of the building, Pt is the overpressure at time t, CD is the drag coefficient of the building to wind pressure (CD = 1.2 for a rectangular building), and qt is the dynamic pressure at time t. This 19 cm computed maximum deflection allows us to estimate how much energy is permanently and irreversibly absorbed from the blast wave by a building. If the effective loading pressure (overpressure and dynamic pressure combined) on the building for the first 0.5 second is equal to 12 psi (83 kPa) then the mean force on the building during this time is 13 million Newtons, and the energy absorbed by the building from the blast wave (reducing the potential of the blast to cause further destruction at greater radial distances) is simply:
E = Fx = 13,000,000*0.19 = 2.6 MJ.
Although you might expect some overpressure to diffract downwards as the energy is depleted near ground level, diffracted blast pressures are lower than incident blast pressures. In any case, dynamic pressure is a directional (radial) wind effect which does not diffract downwards like the overpressure does. Hence, blast energy loss from the wind (dynamic) pressure cannot be compensated for by downward diffraction. This is why shallow open trenches provided protection against wind drag forces at nuclear tests in the 1950s, although the overpressure component of the blast did diffract into them.
The Home Office Scientific Advisory Branch blast expert was Frank H. Pavry, who like Penney had been to Hiroshima and Nagasaki to assess the blast effects there, and had also attended the 1952 British nuclear test, Operation Hurricane, where he exposed 15 WWII 1939-designed Anderson civil defence shelters, proving their utility against nuclear blast. (A data summary for Anderson shelters at Hurricane is here and here. Note that due to local conditions they used easily blasted sandbags, not packed earth cover, which provides additional blast shielding by the strong "earth arch" effect.) Pavry in 1957 summarized the secret data on blast height of burst effects, including the thermal effects from the precursor, in Report of a course given to university physics lecturers at the Civil Defence Staff College 8-11 July 1957, UK National Archives document HO 228/21. For example, the 1957 edition of TM 23-200, Capabilities of Atomic Weapons, shows that the classical Rankine-Hugoniot equations relating overpressure and dynamic pressure are false when blast energy is absorbed by the sand-storm "precursor" blast effect (Figures 2-9A, 2-10A, 2-13 and 2-13): for a 1 kt nuclear burst at 300 ft height, the ideal surface 15 psi peak overpressure range is reduced by from 315 yards to 210 yards by the precursor, while the peak dynamic pressure is increased at 200 yards range from 20 psi for an ideal surface to 60 psi for the precursor. In other words, the blast wave parameters are very susceptible to the effect of loading by sand and dust, sent into the air near the ground by the thermal pulse. (Pavry also proved the nuclear blast protection of the London underground tube system, in 1963. In addition to Pavry, WWII shelter expert Leader-Williams assessed the nuclear test data and applied it to prove how to minimise casualties in a nuclear war.)
This continuing British secrecy is worse for EMP, fallout, and thermal burns and fire effects (see previous post for thermal burns exaggerations versus real data), fully explaining why the public is so deluded on nuclear weapons effects today. CND anti-nuclear biased propaganda supporters like Phil Bolsover and Duncan Campbell simply assumed that misleading American data disproved British civil defence, which - because the supporting nuclear test evidence was secret - was assumed to be badly informed guesswork. The conflict between the British and American height of burst curves is down to some of the thermal energy being incorporated into the blast, increasing the effective blast yield. This effect is easy to compute mathematically, because it's the same kind of calculation used to compute blast waves from the neutron bomb, where the neutrons heat up the air prior to the blast wave travelling through it and picking up energy from the hot air. So what you're basically doing is adjusting the effective blast yield of the air burst nuclear weapon, by adding to it a fraction of the thermal radiation energy, namely that intercepted by the ground prior to the arrival of the air blast at the location of interest. This greatly enhances the purely hydrodynamic Mach region blast reflection effect. (In a surface burst, most of the thermal rays run parallel to the ground and are not intercepted by it, so there negligible enhancement of the blast wave by the thermal flash.)
Penney obtained very good blast overpressure data for British free air bursts of about 1 kt and 15 kt yield in Maralinga, which were high enough above the ground to prevent the desert sand being popcorned (the "precursor" blast wave), so that thermal effects were isolated and the surface hot air heating contribution to the blast wave could be correlated with the data from a series of scaled low yield AWRE conventional TNT air bursts over a concrete heat-reflecting surface in England. (This explains the fact that the British nuclear weapons handbook shows less of a blast enhancement for air bursts than Glasstone does, a trivial issue that led to complete nonsense from Phil Bolsover, Duncan Campbell, and the Marxist militant group within the a political trade union called the British Medical Association, which produced an ill-informed report on nuclear war in 1983, which exploited Thatcher's continuing secrecy on British nuclear weapon test effects.) The April 1980 Kaman Sciences Corporation Handbook for Nuclear Weapons Effects under Arctic Conditions, AD-A197814, in Figure 2-17 confirms the validity of the Penney's UK AWRE (Atomic Weapons Research Establishment) blast wave height-of-burst analysis, by comparing the AWRE curves to conventional explosive data from three American laboratories (Naval Ordnance Laboratory, Sandia Corporation and Ballistic Research Laboratories):
John von Neumann came up with the first theory to predict the oblique or Mach stem blast "reflection" effect in his 1943 report for the U.S. Bureau of Ordnance, Oblique Reflection of Shocks, Explosives Research Report 12, but this "three shock" (Mach "Y" stem) theory tended to exaggerate the pressures observed for nuclear weapons even in ideal conditions on unobstructed deserts. An alternative theory was that the Mach region overpressures for air bursts should be similar to those in a surface burst (since the Mach wave is a composite of incident and reflected pressures, as occurs for the hemispherical blast in a surface burst), with a slight enhancement for the fact that energy lost in surface burst cratering is available for blast. However, this theory underestimated the observed pressures. It now seems clear that the latter theory is useful, if a simple allowance for thermal heating of the surface is made. Up to half the thermal yield of an air burst can be absorbed by the ground, and since only a small fraction of the blast wave travels near the ground, the thermal heating of the surface by an air burst effect can give a considerable boost to the effective blast yield to use in predicting peak overpressures over the ground.
The fallout threat assessment
Because the fallout patterns from British nuclear tests were irregular in shape, Britain never got into the American muddle of using idealized cigar shaped "fallout predictions" (these originated from the fact that the first ever American surface burst test, 1.2 kiloton Jangle-Sugar in 1951, occurred in a simple wind structure, thus setting up a dogma of simplistic analysis). The British basis for fallout area predictions is explained by George R. Stanbury's 1959 report, CD/SA 101, Downwind fallout area from groundburst megaton explosions, which compares the fallout areas given by Dr Frank H. Shelton in his June 1959 testimony to the Congressional Hearings on the Biological and Environmental Effects of Nuclear War, with Glasstone's 1957 Effects of Nuclear Weapons, and with the November 1957 Confidential-classified American TM 23-200, Capabilities of Atomic Weapons (which by 1959 was in British hands, part of an exchange deal). Stanbury notes that Shelton's data was probably quoted directly from TM 23-200. He also notes that the Confidential TM 23-200 gives smaller fallout areas than Glasstone's book. The figures for fallout areas which Stanbury chose to go into the 1959 edition of Nuclear Weapons were from Glasstone 1957, not TM 23-200, however only areas are given, which are less sensitive to wind conditions than distances. This is because the fallout contours generally become narrower when the wind speed is increased, so the area covered is often the same (however this is not always true, since a very strong wind can spread out the fallout over such a large area that the very high dose rate contours which occur in light winds disappear completely).
For example, Capabilities of Atomic Weapons, TM 23-200 (1957) Figures 4-15B and 4-16B for a 1 megaton fission surface burst in a simple 15 knots wind pattern gives at 1 hour a dose rate of 3,000 R/hr extending 12.5 statute miles downwind, with a width of 3.0 miles. This can be directly compared to Glastone, Effects of Nuclear Weapons 1957, Table 9.71, which states the downwind distance for this case (15 statute miles per hour, which is nearly 15 knots since a nautical mole is 6076 feet, compared to 5280 ft for a statute mile) is 22 statute miles, and the width is 3.1 miles. Thus, Glasstone shows a much larger fallout area than the classified book. According to Figure 4-4B in Capabilities of Atomic Weapons, TM 23-200 (1957), for a 1 megaton fission weapon and 15 knots wind the 1 hour reference time 3,000 R/hr fallout contour covers an area of 26 square miles, but Stanbury, following Glasstone 1957, selects a figure over twice that large, 54 square miles, shown in Table 15 of the 1959 Nuclear Weapons (for this small distance from ground zero, the fallout is soon deposited so that 3,000 R/hr at 1 hour is equivalent to 300 R/hr at 7 hours after detonation, due to the rapid -1.2 power of time decay rate of fallout). This figure is modified to 20 square miles in Table 13 in the 1974 edition, purely because of the decision to use a 50% fission yield for fallout from thermonuclear weapons.
Fallout of 3,000 R/hr at an effective arrival time of 1 hour gives 8,085 R during the first two days, which is reduced to 8,085/40 = 202 R in a typical British brick house refuge room with windows blocked (protection factor 40) or 40 R or less in an outdoor earth-covered trench shelter (protection factor 200 or more). At this time, 48 hours after detonation, the dose rate has fallen by natural radioactive decay from the 1 hour level of 3,000 R/hr to just 30 R/hr, which would allow evacuation towards the upwind or cross-wind direction, as organized by the Cold War Civil Defence Corps for all "Z zone" areas where the dose rate at 48 hours is above 10 R/hour, as documented in Manual of Civil Defence, Radioactive Fallout: Provisional Scheme of Public Control.
People could return even to this most highly contaminated "hotspot" at 14 weeks after detonation, when the dose rate would be down to just 0.3 R/hour and still decaying, a factor of 10,000 times smaller than the 3,000 R/hour at 1 hour. Contrast this 20 square miles area of inconvenient fallout hazard from a 50% fission 1 megaton surface burst (requiring merely a 48 hour indoor stay and the evacuation for 3 months) to the American propaganda by people like Dr Ralph Lapp and Lewis Strauss about a danger area of 7,000 square miles following the Bravo test of 1 March 1954. That was based on people remaining outdoors, with little clothing, and making no effort to decontaminate themselves or the area they are in for the entire period of exposure. As proved in earlier posts (for example here, here, here, etc.), a dose of 40 R at Hiroshima and Nagasaki was insufficient to even merely double the normal very small risk of leukemia, so if you did get leukemia after receiving 40 R in Hiroshima it was about 75% likely to be natural, not due to radiation (as proved in the previous post). With other forms of cancer (solid tumors), the increase in natural risk was even smaller than it was for leukemia.
Once people return after 3 months to an area at an outside dose rate of 0.3 R/hour, they can decontaminate it, by road sweepers to remove dust and water hosing to wash fallout off roofs into drains, where the gamma radiation is shielded from people, as explained in paragraph 11.26 of the 1959 Nuclear Weapons book, which is backed up by the 1959 Home Office Scientific Advisory Branch report CD/SA96, The decontamination of residential areas, which compiled nuclear test data tables on decontamination (from the USNRDL 1958 report Radiological Recovery of Fixed Military Installations, and other nuclear test fallout research reports). This gives decontamination effectiveness data for land and ocean burst fallout on different surfaces (deep plowing to reduce dose rates and the addition of potassium chloride to soil to block cesium-137 uptake by plants is used in agricultural areas). A further report in 1965, SA/PR-97, The value of area decontamination in reducing casualties from radioactive fallout, originally secret, planned even earlier decontamination by fire-hosing residential areas where the 1-hour reference gamma dose rate was 500-3,000 R/hr. The report finds that at levels of fallout below 500 R/hr at 1 hour, there are few casualties indoors in Protect and Survive handbook type "inner refuges" anyway (200 R producing a casualty), while higher levels than 3,000 R/hr at 1 hour tend to expose decontamination crews to excessive doses even 5 days after detonation, so evacuation is then a better option. The report shows that human-crewed decontamination work becomes feasible at 1-5 days after detonation, when the 1-hour outdoor dose rate of 500-3,000 R/hr has decayed to 10 R/hr. Decontamination crews restricted to areas below 10 R/hr cannot get more than 10 x 8 = 80 R in an 8 hour shift. (Obviously, modern technology would allow road sweeper/flusher trucks to be equipped with drone-type full remote control and cameras, reducing hazards.)
Therefore, the real fallout inconvenience encompasses an area less than the area of hazard from high velocity flying glass, even before you look at the reduced fallout doses from cleaner weapons with lead or tungsten fusion stage pushers in place of uranium-238, e.g. the comparisons of measured fallout in Operation Redwing weapon test report WT-1316 Table 2.11, showing that the maximum 48 hour land equivalent fallout dose downwind of 3,000 R outdoors (unshielded) covered an area of 520 square miles for 5 megaton 87% fission Tewa (a thermonuclear test at Bikini Atoll in 1956), compared to just 20 square miles for the clean bomb test, Navajo, which was just 5% fission but had a similar total yield of about 4.5 megatons (also at Bikini Atoll in 1956). Although Navajo was fired on a barge, the plot in Fig. 2.45 of the report using four different Redwing nuclear tests shows that the fallout areas only depended significantly on the fission yield, not the surface the bomb was exploded on or the wind.
Therefore, if anyone in politics has radiophobia, they can simply make our bombs cleaner (5% fission like Navajo, or 15% fission like Zuni, a 3.53 megaton test also fired in 1956). The enemy can be coerced into doing the same thing, because our protected second strike retaliation capability means that our deterrence doesn't require instant retaliation; we can wait to check if the apparent attack was just a meteor explosion, or a flock of birds on a radar, or a missile test by North Korea. Similarly, we can check the fallout to determine the bomb design and the fission yield, just as we did when Russia was testing in the atmosphere. If someone detonates a nuclear weapon which produces a lot of lingering contamination, we will take that into account in determining the reply. The 1961 Russian test of 50 megatons proves that was clean: we detected fission products from only 1.2 megatons after that test, proving a fission yield of 2.4%. Therefore, an enemy with a thermonuclear capability can potentially replace uranium-238 in the fusion stage with lead or tungsten, which have sufficient ablation density to compress the fusion fuel, without producing the large radiation doses you get from uranium-238 fission (neutron capture in an inert pusher contributes only trivially to the fallout hazard, as proved by Redwing weapon test reports WT-1316 and WT-1317).
If anti-clean nuclear weapons propaganda from politically biased people can be replaced with the truth, the experimentally proved facts of physics, then collateral damage can be averted even in a war, just as Hitler was discouraged from attacking England with kilotons of tabun nerve gas in V1s and V2s.
Another fallout controversy George R. Stanbury studied was the close-in fallout within the actual damaged area (reports CD/SA87 December 1957, classified Confidential, which we reviewed in detail here, and CD/SA94 which defends the upwind fallout predictions in the 1959 booklet) since that is precisely the area that civil defence search and rescue teams would need to work in. The close-in fallout around the crater was found to be much heavier in the 1952 Mike test where the bomb had a massive steel case (a total bomb mass of 82 tons, well beyond any airborne delivery system), which formed the basis for heavy upwind fallout dose rate predictions from megaton weapons in Glasstone 1957. However, when the upwind fallout data from the light aluminium-cased 1954 Castle and 1956 Redwing nuclear weapons trials was assessed, the upwind dose rates in the blast damaged area for similar fission yields and distances were found to be only 10% of those for Mike for land surface bursts and only 1% for ocean water surface bursts. The main downwind fallout pattern dose areas were similar for both types of burst, note however that the map scales for the Bikini Atoll for upwind fallout in reports WT-915 and DASA-1251 are incorrect for Operation Castle and exaggerate the fallout distances by up to a factor of two. Stanbury explains on page 44 of the 1959 Nuclear Weapons handbook, paragraph 8.27:
"The cloud model for the larger weapons indicates that very little fall-out is likely to be deposited upwind beyond the limit of complete destruction, unless the winds at all levels up to cloud height are of exceptionally low speed or are in opposite directions at different heights. ... The situation may vary from complete prevention of fire-fighting and rescue to complete freedom from fall-out in the damaged area beyond the range of complete destruction."
Stanbury in his Confidential December 1957 paper CD/SA87 uses two reports, Edward Schuert of the U.S. Naval Radiological Defense Laboratory in report USNRDL-TR-139 and also Dr Frank H. Shelton in an AFSWP report called Physical Aspects of Fall-Out which gives the in compressed form conclusions about local fallout based on dose rate meters, ocean surveys and rocket probing of the mushrooms for Operation Redwing, i.e. focussing on four thermonuclear weapons exploded at Bikini Atoll in 1956:
"We are forced, therefore, to conclude that the heavy upwind contamination for a wind speed of 15 miles per hour, which is deduced from Table 9.71 of Effects of Nuclear Weapons is incompatible with the presently accepted physical model of the explosion which explains the megaton trial data so well. For lower wind speeds, however, it is clear that contamination could extend further upwind; in the limiting case of still air some contamination could cover the whole area under the mushroom cloud ... Conversely, of course, higher winds would result in less upwind contamination; for example with a wind speed of 30 miles per hour it seems probable that only the largest particles (1000 microns) would fall upwind of ground zero and contamination would not extend outside the area of total destruction."
What is interesting here is that the land based measurements of fallout upwind from Redwing Tewa (5.01 Mt, 87% fission) covered most of Bikini Atoll and so are an extremely useful check on what Stanbury says. The simplistic idea of fallout particles drifting slowly downward would prevent any fallout at all upwind from the detonation in a moderate wind speed, because the mean in the particle size distribution is generally about 100 microns (0.1 mm) and most of the activity is located at the altitude of the base of the cloud, as proved by rockets with radiation meters and radio telemetry, fired through the Zuni, Cherokee and Tewa clouds in 1956. Therefore, even fallout beginning at the upwind cloud base would be expected to be blown downwind of ground zero, before being deposited. You would expect that any fallout which actually lands the upwind area would therefore consist of very large particles, several millimetres in diameter, like hail or heavy rain. However, this is not what was found by Peter Brown and others in weapon test report WT-1311, Gamma exposure rate versus time, Operation Redwing:
They found in Figure 3.18 that at 4.2 statute miles upwind from Tewa, although fallout started at just 15 minutes after detonation, the fallout took 3 hours to reach a peak of about 100 R/hr (after correction for instrument shielding protective factor of 1.4). Clearly, only small fallout particles would still be airborne at 3 hours after detonation, and you would expect that even moderate winds would have blown then downwind prior to being deposited. What seems to be the case is that, as Stanbury explains in the quotation above, with a large angular wind shear, winds blow in almost opposite directions at different altitudes, so the particles don't fall continuously in the overall downwind vector wind direction, but instead zig-zag upwind and downwind as the fall through successive wind layers. Therefore, some very small particles end up moving hardly any net downwind distance as they slowly fall through layers of opposing winds.
But there is another issue for close-in fallout, the downdraft around the toroidal vortex fireball as it rises:
In the 11 May 1959 issue of Life magazine, RAND Corporation fallout researchers Stanley Greenfield and Robert Rapp were pictured (photo above) modelling smoke rings against a blackboard, a piece of classical physics that goes back to the vortex atom theory of Lord Kelvin, who noticed that smoke rings showed stability and would bounce off each other when collided, so that in a perfect fluid which he called the ether (prior to Dr Einstein and the discovery of modern quantum field theory), fundamental particles would be indestructible spinning vortices. Air burst nuclear weapons in Nevada showed the toroidal vortex structure of rising fireballs clearly. Unfamiliarity with smoke rings has led to one 100 metres wide filmed earlier this year in Kazakhstan being falsely attributed to UFOs in a Daily Mail report. The explosion of large round buckets of smoke filled burning fibreglass resin in a factory in China last year produced perhaps the best example ever seen, as reported in the Daily Mail newspaper:
Robert Rapp's research on vortex fireballs is reported in two 1963 Secret-Formerly Restricted Data RAND Corporation reports:
RM-3605-DASA, On the behavior of large, hot bubbles in the atmosphere, and
RM-3788-DASA, Further progress toward a practical theory of nuclear cloud behavior.
Also: R. E. LeLevier, Cloud rise, RM-3822, RAND Corp., 1963, classified Secret-Restricted Data.
(For the basic physics, see Yoshimitsu Ogura's paper "Convection of isolated masses of a buoyant fluid: a numerical calculation", Journal of the atmospheric sciences, v19, 1962, pp. 492-502 or Alan Shapiro and Katherine Kanak, "Vortex Formation in Ellipsoidal Thermal Bubbles", ibid, v59, 2002, pp. 2253-2269.)
Rapp summarizes his results with extracts in his unclassified February 1966 RAND Corporation memorandum RM-4910-TAB, A re-examination of fallout models, which on page 5 explains:
"The buoyant forces come into play to accelerate the hot, low-density fireball upward. However, the fact that the pressure decreases with increasing elevation in the atmosphere results in an intersection of surfaces of constant density and constant pressure. According to Bjerknes's theorem for the creation of vorticity in an inhomogeneous atmosphere, this will cause the formation of the vortex ring that has been observed so frequently in the rising nuclear cloud. Thus, at this point, about 5 seconds after detonation, the fireball has been transformed into the nuclear cloud. All of the radioactive material is contained within this rising cloud. The outer, cooler edges of the fireball can contain no radioactive debris, because there has been no mechanism to transport it to the edge. After the vortex motion and buoyant rise has started, however, the fireball is essentially turned inside out."
Rapp then makes the important point that because the vortex is rising, the stream lines of flow within it are different depending on the frame of reference: if the cine camera is tilted upwards and follows the fireball while it rises, the stream lines of debris motion are perfectly centred around the radioactive ring, but films taken of the same fireball that do not follow it upwards effectively superimpose the motions within the spinning torus with the vertical fireball rise, creating the illusion that the torus of circulation has a larger radius than the glowing radioactive ring as Rapp illustrates in the comparison diagram below:
Rapp notes that "This account of the circulation has been verified by making accurate measurements of the edge of the visible cloud", citing H. G. Norment's Technical Operations Research report TO-B63-102, Final report: research on circulation in nuclear clouds. Allowing for 1 megaton cloud cooling by sucking in cool air and by adiabatic expansion as it rises, Rapp explains on pages 13-14:
"... it can be estimated that the average temperature of the rising mass falls to values close to those of the ambient atmosphere in about one minute. If there is some unmixed air from the fireball within the vortex core, that air would cool only at the adiabatic rate. Such a rate of cooling would reduce its temperature by only 60 % in 2.5 minutes. Thus, the temperature within the rising cloud at 2.5 minutes might range, for a 1 Mt device, from as low as 220 K to as a high as 2200 [citing as the reference for this, his secret report RM-3788-DASA, 1963]. ... Cooling by mixing and adiabatic processes destroys the cloud's buoyancy, friction destroys its circulation, and work against gravity destroys its vertical kinetic energy."
Above: Rapp computes a downdraft velocity of 626 miles per hour at a radius of 2.6 miles, 2.25 minutes after a megaton surface burst. As explained in American nuclear weapon test reports WT-4 and WT-615, this downdraft around the central updraft explains the existence of small particles in upwind fallout. Dust is sucked up by the central updraft, carried around the radioactive smoke ring, and is then blown downwards at the periphery. This explains why the gravitational settling rates contradict observed levels of fallout in the damaged area around ground zero, and explains some aspects of the fractionation of fission products. Radioactive gases like krypton-89 (which has a half life of 3.18 minutes) remain in the central hot smoke ring, which explains why their decay products (Rb-89 and Sr-89 in this example) are depleted from local fallout and concentrated in the distant fallout of very small particles.
On the other hand, metal oxides with high melting points like plutonium, uranium, Y-95, etc., condense into solid particles after just a few seconds and can get flung out of the rapidly rotating toroid by the centrifuge effect, where they are then able to collide with, and stick to, the surfaces of dust particles which have been sucked into the fireball by the central updraft. This centrifugal separation of particles from gases in the rapidly revolving toroidal cloud is why the fallout that lands near ground zero is enriched in refractory decay product chains like Zr-95, Nb-95, Mo-99, etc., and depleted in volatile isotopes of iodine, and strontium and cesium which have the gaseous precursors at early times, krypton-90 and xenon-137 (Dr Carl F. Miller explains this centrifugal fractionation mechanism in volume 1 of Fallout and Radiological Countermeasures, 1963).
Rapp explains on page 30 that for a 1962 Nevada test (Johnie Boy), 95 % of the strontium-89 was still in the cloud at 20 minutes after burst, whereas only 28% of the Zirconium-95 remained in the cloud. This is precisely because strontium-89 has the krypton-89 gaseous precursor in its decay chain, which keeps it in the vortex for several minutes while most of the fallout is being formed, whereas the precursor of zirconium-95 is a solid not a gas, so it gets thrown out of the vortex by the centrifuge effect and comes into contact with the desert dust, to form fallout:
"This analysis indicates that there is a great deal of separation of isotopes with particle size, refractory elements being concentrated in large particles and less refractory elements being concentrated in small particles."
Rapp points out that fallout samples collected near early Pacific H-bombs had a log-normal particle-size distribution used in RAND report RM-2148 (mean of 3.8 log microns, standard deviation of 0.69 log microns) that included some smaller particles, yet no where near the true abundance. This was because the samples landing near ground zero were biased in favor of larger particles (a skewed distribution, or statistical error). Rapp makes this error graphically crystal clear in his Figure 10:
This particle size fractionation effect was studied at British nuclear tests for civil defence purposes. For example, the ship harbour burst Operation Hurricane in 1952 gave highly soluble fission products in fallout containing sea water and black iron oxide produced in the fireball from the steel of the ship, whereas for bursts over silicate topsoil at Maralinga in 1956, the volatile fission product decay chains plated the outer surfaces of the particles, and were relatively more soluble than the metallic oxides which ended up trapped inside the melted particles. Table 27 in Dr John Loutit and Robert Scott-Russell's nuclear test fallout report AWRE-T57/58 shows that the water solubility of Buffalo-1 silicate soil fallout was 80% for strontium nuclides (-89, -90, etc.) and iodine nuclides (-131, -132, -133, -135), 40% for Ba/La-140, 35% for Te-132 and Mo-99, 5% for Zr/Nb-95, and only 3% for Ru/Rh-103. Thus, “fallout solubility” depends entirely upon the nuclide involved. It is therefore misleading to quote a percentage solubility figure without saying which nuclide is referred to. If you do quote an overall percentage for solubility, you have to say whether it is for beta or gamma radiaton and the time after burst, because the relative contribution of soluble nuclides varies with time. Plutonium oxides are almost entirely insoluble, whereas iodine is almost completely soluble because they are on the outside of the glassy particles.
AWRE-T57/58 shows that a total of 15% of the Buffalo-2 fallout was retained by pasture grass, mainly in the stem base. Table 15 in the report shows that threshing wheat after Buffalo-2 left 90% of the fallout on the husk of wheat and only 10% remains on grain after threshing, and the authors spell out the implications:
“At a dose rate of 50 R/hr at 1 hour, 80 kg of flour would contain only 0.06 microcurie of Strontium-90. ... The hazards arising from the consumption of contaminated flour appear therefore to be smaller by a factor of more than a thousand than those arising from milk.”
The Buffalo-2 result that only 10% of fallout gets through through the threshing process to contaminate the flour is stated in paragraph 10.16 of the 1974 edition of Nuclear Weapons, but AWRE-T57/58 is not cited and there is no indication provided that this fact comes from an actual nuclear explosion experiment, done at great cost. Consequently, the data does not appear impressive to readers, who are left unaware of whether the facts are guesswork or actual evidence. This is a fatal situation for such a controversial subject.
Likewise paragraph 10.20 points out simple well proven countermeasures to the iodine threat. Limiting fallout contaminated milk consumption for a month after a nuclear explosion is an adequate countermeasure for ingested fallout, while the iodine-131 decays. Contaminated milk need not be wasted: it can be frozen, powdered, or processed into cheese or ice-cream that can be stored for a month while iodine-131 decays with its 8 days half-life, during storage. Alternatively, cattle can be kept in barns on winter fodder while the iodine-131 decays on fields outdoors. Temperature has no effect on radioactive decay, so it is safe to freeze radioactive fallout contaminated food while it undergoes rapid radioactive decay. Fallout uptake by the roots is relatively small and was well investigated in American nuclear tests.
Robert Scott Russell of the Agricultural Research Council, Radiobiological Laboratory, England, after analyzing the nuclear fallout in Maralinga wrote an interesting paper called "The Extent and Consequences of the Uptake by Plants of Radioactive Nuclides" which was published in the Annual Review of Plant Physiology, volume 14 (June 1963), pages 271-294:
“Iodine-131 is ... of concern primarily as a source of exposure of infants who consume appreciable quantities of fresh milk, partly because of the very small size of their thyroid glands in which it is concentrated, and partly because milk is usually the most highly contaminated food. Doses to infants from iodine-131 have on occasions been considerably higher than those from any other component of fallout; for example, towards the end of 1961 it was estimated from the analysis of milk that the thyroid glands of infants fed on fresh milk in the United Kingdom would have received about 170 mrems. ...
"Caesium-137 which was deposited on foliage of plants appears to be retained relatively similarly to strontium 90, and like strontium it is readily removed from foliage by rain. The concentration of caesium-137 within different tissues which results from direct contamination, however, can contrast very markedly with that caused by strontium-90. This is due to the mobility of caesium-137 within tissues; thus nearly 30% of the caesium-137 which has been deposited on the foliage of potatoes may reach the tubers, as compared with less than 1% of strontium-89 ...
"Plutonium. Because of its very long half life and high toxicity to animals consideration has been given to the entry into plants of the fissile element plutonium. A very slow rate of absorption is to be expected because it forms high valency (usually 4 or 6) ions; this has been confirmed in several studies and, over 1.5 years, grass grown in pot culture may absorb less than 0.0001% of that added to the soil.”
For these reasons, root uptake is not a problem as long as there is enough potassium in the soil to saturate it and deter cesium-137 uptake (potassium chloride can be added to the soil if not). Growing potatoes minimises strontium-90 uptake. In any case, because of fractionation, iodine, cesium and strontium are reduced in local fallout, which is enriched in insoluble nuclides which are not a root uptake problem, such as plutonium. The water soluble root uptake nuclides concentrate in the tiny particles of global fallout, so that problem is dispersed around the world like the 170 megatons of atmospheric nuclear test fallout, which was well studied: even iodine-131 to kids thyroids proved to be insignificant, compared to the large doses needed to significantly boost the natural incidence of thyroid cancer.
Scott Russell explained in his paper in the massive 1970 symposium, Survival of food crops and livestock in the event of nuclear war there is no significant problem from root uptake in a nuclear war. Even if a thunderstorm causes heavy rainout, the heavy rainfall helps to decontaminate it, by washing it either deep into the soil where it is shielded, or into storm drains, where it is again shielded. It has proved trivial compared to the external gamma ray dose soon after detonation! For this reason, the 1974 Nuclear Weapons book shows how to decontaminate food by washing or peeling the layer with fallout off or discarding pea pods and the outer leaves of cabbage.
Moving on the radiation dose calculations, the Home Office Scientific Advisory Branch report CD/SA45, Gamma radiation dose rates at heights of 3-3000 feet above a uniformly contaminated area, incorporated scattered gamma rays into the Samuel Cohen's RAND Corporation calculations of the dose rates above contaminated areas, which had been published as an appendix to Glasstone's 1950 Effects of Atomic Weapons. This is also the origin of the British calculating scheme for protective factors of buildings. On a flat plane, about 90% of the 0.7 MeV gamma dose at 3 feet height comes from direct gamma rays from the ground and since the gamma rays have a long range, most of this radiation is coming almost horizontally, while 10% is air scattered and is thus coming from many directions in the sky. The radiation dose in a building can therefore be calculated utilizing this geometry, making suitable allowances for roof contamination which depends on the roof angle and rainfall (CD/SA 103) and fallout ingress. These factors are in most cases less important than the assumption used about the gamma ray energy. Dr Triffet disclosed at the June 1959 congressional nuclear war hearings that for close-in land burst thermonuclear fallout, the gamma ray energy during the sheltering period for a week or two after burst drops to just 0.25 MeV due to Np239 and U237 formed in the U238 jacket.
This means that during the main sheltering period, any building offers far more protection against fallout than predicted using the usual assumption of 0.7 MeV from Glasstone, 1 MeV for calculations using the 1 hour energy, or 1.25 MeV for experiments using cobalt-60 sources (which emit two gamma rays, 1.17 and 1.33 MeV, giving an average of 1.25 MeV). Stanbury like Triffet predicted large contributions to fallout radiation during the sheltering period from low energy Np239 using British nuclear weapon trial Operation Totem and Hurricane neutron capture data, in his 1959 report R and M 75. Ignoring this low energy of the gamma rays offsets the errors of ignoring fallout ingress effects. What percentage of rainfall normally enters a house? If the windows are open, some will on the side facing the wind, landing on the window sill and maybe the floor nearby. However, while sheltering, people can use a damp cloth or mop to clean up and throw out any dust that enters. There are cleaning devices in every house to decontaminate fallout: dust cloths, paper towels, vacuum cleaners, brushes, etc. The idea that people are going to stay indoors for two weeks of sheltering without finding the time to clean up any fallout ingress is clearly the usual biased scare-mongering of political anti-nuclear fanatics.
John Newman examined effects of fallout blown into a buildings, due to blast-broken windows, in Health Physics, vol. 13 (1967), p. 991: ‘In a particular example of a seven-storey building, the internal contamination on each floor is estimated to be 2.5% of that on the roof. This contamination, if spread uniformly over the floor, reduces the protection factor on the fifth floor from 28 to 18 and in the unexposed, uncontaminated basement from 420 to 200.’
But measured volcanic ash ingress, measured as the ratio of mass per unit area indoors to that on the roof, was under 0.6% even with the windows open and an 11-22 km/hour wind speed (U.S. Naval Radiological Defense Laboratory report USNRDL-TR-953, 1965). So Newman's 2.5% assumption is a severe exaggeration of the ingress problem.
A problem occurs for the cobalt-60 bomb, popularized by Stanley Kubrick's film and many books and papers, starting with Leo Szilard in 1950 during his fanatical anti-H-bomb campaign. (Szilard couldn't imagine a U238 jacket, which is effective, only an ineffective Co-60 jacket.) Cobalt-60 was included in an Operation Antler test in 1957, resulting in the Co-60 remaining only in large metallic pellets, millimetres in diameter, which landed in the vicinity of ground zero. This is because cobalt has no gaseous precursors, so it is highly refractory and lands in large particles near ground zero. Little ends up in global fallout, which is depleted in refractory nuclides and enriched in volatiles. In any case, the long half life (over 5 years) results in very low specific activity. As explained, Co-60 emits two gamma rays totalling 2.5 MeV for every neutron captured in cobalt-59; using the same neutron to split U238 gives 200 MeV, i.e. 80 times more energy, including far more residual radioactivity, some of which is volatile nuclides which does get into global fallout. Finally, even if someone was to set off a massive Co-60 bomb as the film On the beach imagines, the slow build up of the radiation gives plenty of time to decontaminate it before receiving an significant dose (the same applies to nuclear reactor fallout). Scare-mongering relies on trying to divert attention from genuine countermeasures and physical understanding, towards political activism like banners, shouting, hate attacks, marches, and a fear based culture. Nuclear physics is being made part of old horror film culture.
Debunking of fire storm and thermal burns exaggerations, due to thermal radiation shielding
In Hiroshima and Nagasaki, air scattered thermal radiation did not prove effective in causing burns or starting fires: only skin or dry kindling exposed with a direct view of the fireball (no intervening trees, people, or buildings) were burned or ignited. George R. Stanbury investigated this thermal shadowing effect in detail for British cities, as we documented in previous posts. The 1959 edition of Nuclear Weapons states the conclusions on page 28:
"In a built-up area ... even from a high air burst the buildings would have a considerable shielding effect on one another [once the distance from ground zero is several times the optimum burst height, the thermal rays are coming almost horizontally and will be intercepted and stopped by the first buildings they arrive at]. ... A firestorm only occurred ... where at least every other building [50% of buildings] in the area has been set alight by incendiary attack. ... studies have shown that a much smaller proportion of buildings than this would be exposed to heat flash (due to shielding). Moreover, the vulnerable centres of many British cities were destroyed in the last war and the new buildings which are replacing them are mainly of fire-resistant construction and less closely spaced."
The British WWII improvised shelters against fire (incendiary bomb effects), blast and gas effects were applied to nuclear weapons survival after verification by nuclear test experiments. Similarly, the Swiss Federal Authority's Office of Civil Defense applied similar techniques for sealing up doors and windows against blast, heat and fallout to those used in WWII refuge rooms in buildings and in Cold War nuclear civil defense, in their 1977 handbook, Technische Anleitung für die Herrichtung von Behelfs schutzräumen (TA BSR 1977), which translates as Technical Instructions for the fitting-out of makeshift shelters:
Update (1 July 2015)
"In fact, I basically designed the first boosted bomb device. ... I got interested in what's called nuclear effects, the effects of nuclear explosions. In fact, I really got interested in that in 1962 when we had the high altitude test series, Operation Dominic. And I started working in that, and it turned out that the AEC, or Los Alamos Laboratory, was not really very interested in the effects of nuclear explosions by that time. In the early days, they had done a lot of good work on blast and shock and fallout and that kind of stuff. But by that time, most of the people there regarded their main job as putting bombs in the stockpile, and there wasn't too much appreciation that it was important to understand about the physics of nuclear effects, for example, EMP. ... way back in the 1970s, early seventies, there was a fellow at the RAND Corporation, this is after the RDA physics group [Harold Brode et al] left. His name was Cullen Crane [see illustration below], who, I don't know if you've ever heard of him—well, anyway, this fellow was saying that EMP is a hoax. These guys are either crazy or they're doing it to, you know, perpetuate their salaries. And so the Jason group got tasked by DNA to look into this. Now, in this case, in my opinion, the Jason group didn't do a very good job, because instead of reading the reports and trying to settle the argument, they started out from scratch and first did their own version of EMP, and at least, I didn't think that was necessary at the time. ... They do not, you know, when they begin to look into something, they don't go back and make sure that they've read all the earlier references and stuff like that. But you don't expect physicists to be your formally good historians."
- Dr Conrad Longmire, interview given to American Institute of Physics's Finn Aaserud, 30 April 1987.
The attack quoted above by Longmire on RAND Corporation Cullen M. Crain's alternative method of calculating EMP, by summing individual electron EMP emissions rather than solving Maxwell's equations, seems a bit over the top. Yet that is the standard, very paranoid, response which often greets alternative theories in physics. Crain's unclassified version of the 1973 paper, his 1982 Calculation of Radiated Signals from High-Altitude Nuclear Detonations by Use of a Three-Dimensional Distribution of Compton Electrons (DTIC ADA114738 or RAND N1845) gives results that agree with other more standard techniques in the applicable cases. There is a tendency to be extremely defensive about the first theory to arrive on the scene, to the point of trying to use it to close down efforts to work on alternatives! If you have an alternative idea, you first try the polite method, but you get brushed off rudely, like a fly. Then you give them a taste of their own medicine, and they have the temerity to call you rude! This is a pretty standard problem. Whatever approach you take, some contrived, specious excuse is used to silence it.
High altitude EMP data is compiled in an earlier post, linked here. The January 2014 issue of DTRIAC Dispatch discussed late-time EMP, which is extremely low frequency (ELF) and therefore penetrates some metres into dry ground, where it couples to very long cables. What's generally more dangerous is the early time or E1 phase of the EMP which delivers frequencies up to 100 MHz, in the UHF spectrum, with intensities of up to 50 kV/m for a fraction of a microsecond. The problem is that although EMP effects from a 1.4 megaton burst at 400 km (Starfish) in 1962 are well known, the correct scaling laws for the terrorist threat from say North Korea detonating 7 kt (the yield of its last nuclear test) at say 100 km altitude, are not openly discussed. EMP Theoretical Notes are now online, and they document the early-time EMP research by people like Conrad Longmire of Los Alamos, who is credited with being the first to understand the Starfish EMP from 1962, where the earth's magnetic field deflected Compton electrons, producing an EMP. (Glasstone discusses EMP in the April 1962 edition of The Effects of Nuclear Weapons, but not that mechanism.) Longmire's EMP mechanism was first published openly by RAND Corporation's Karzas and Latter, report RM-4306 (DTIC document AD607788), crediting him.
The only published paper giving plots of early EMP peak field strength versus yield (of prompt gamma rays escaping from the weapon) and burst height is the Master's Thesis of Louis W. Seiler, Jr. His plots show a generally very weak and complex dependence of yield and burst height on the EMP. The problem with numerically integrating differential equations with a computer is the lack of understanding that results. This problem also plagues weapons design and other nuclear effects computer codes. Hence, there is a need to try to come up with analytical solutions. Naively, you might take the equation for electromagnetic wave energy density in terms of field strength (energy per unit volume is half the product of the permittivity of free space, and the square of the electric field strength), and give the EMP a volume equal to the that of the prompt gamma ray pulse (a 10 ns pulse for instance is a shell 3 metres thick, since the gamma rays and EMP are going at light velocity which moves 3 m in 10 ns). This gives a simple formula where EMP field strengths are proportional to the square root of the yield, divided by the distance from the bomb. This naive theory is completely misleading, largely because the Compton current is largely cancelled out by an opposing conduction current, at least for small distances (between bomb and atmosphere), and large yields. (In addition, you need to take account of how far the Compton electrons travel before absorption in the air at the altitude in question, in comparison to the their gyro radius in the geomagnetic field.) However, Karzas and Latter found an analytical solution to this conduction current limitation of the EMP in their equation 52 (the symbol sigma is the air conductivity, signifying the conduction current term in equations 51 and 52):
I've highlighted the two key parts in red. The first is ellipse covers the Compton current contribution, basically the Compton current density j integrated over a radial line through the deposition region, with the EMP also inversely proportional to distance. The second term, multiplying the first, is a exponential attenuation factor for the effect of the conduction current. In fact, this general analytical solution to the EMP first appears in equation 12 of another RAND Corporation paper on EMP issued more than a year earlier, W. Sollfrey’s RAND Corporation report RM-3744-PR, An Analytically Solvable Model for the Electromagnetic Fields Produced by Nuclear Explosions, July 1963, EMP Theoretical Note TN53. This analytical solution was generally ignored or solved numerically, and was not simplified into a simple model for EMP field strength calculations. Our argument is that it can be simplified with good approximations (such as taking the air conductivity to be constant through out the gamma ray deposition region "pancake" under the burst), to give a simple model to explain Seiler's curves. Moving ahead to 1987, Longmire and others reinvent the wheel (in separate parts!) in equations 9 and 10 of EMP Theoretical note 354:
Longmire's 1987 EMP theoretical note in a way helps by breaking the product into two parts that can be multiplied together. Each part, Compton contribution and conduction current, lead to questions and answers that are very important. First, EMP like radio is the time-derivative of the net current, not its integral (the opposite of taking a derivative!), so how can you get a correct result from equation 9?
The answer to this is profound for Maxwell's theory of electromagnetism, for it means that Longmire's EMP, radiated due to the sideways deflection of Compton electrons travelling at nine-tenths of velocity of light, is showing us how radiation really occurs, in all cases. There's a duality between Gauss's law of static charge (the radial electric field) and electromagnetic radiation due to charge acceleration. In other, plainer, words: when the Compton electrons are deflected sideways, part of their radial field (modelled conventionally by Gauss's law!) is converted into synchrotron radiation. Conventionally, Maxwell's equations say that the radiation from an oscillating charge is not the Gauss field (see for example, equation 28.3 of the Feynman Lectures on Physics, volume 1, where separate terms are given for fields due to charge acceleration and static charge).
Take mass and energy. They were once considered completely different. Then it was discovered that under certain conditions, significant conversions between them could occur (e.g. in fission and fusion). By analogy, the validity of Longmire's result means that the Gauss field and electromagnetic radiation are the same thing in certain conditions. What we're pointing out here is that if you have an electron moving at 0.9c and deflect it sideways by a magnetic field, the Longmire equations prove that some of its c-velocity Gauss field is being sheared off, and is continuing along its original path without deflection. That's the mechanism of electromagnetic radiation by accelerating charge.
The lost field energy from the electron then appears as a deceleration of the electron (loss of kinetic energy). This is proved by the very fact that Longmire's proof-tested equation must be a duality to Maxwellian synchrotron radiation. In quantum field theory, the Gauss field isn't static at all but is composed of light velocity exchange radiation, virtual photons (electromagnetic gauge bosons). So this really makes the case for understanding the Maxwell equations in terms of moving virtual photons; it's obvious that these virtual photons become real photons (observable radio waves or EMP, for instance) when the charge is accelerated, breaking the normal equilibrium of exchange of virtual photons between charges, which constitutes the field extending throughout space.
Secondly, this analytical solution provides easy predictions of EMP, explaining Seiler's graphs. Here are the first couple of pages from my draft paper on this topic, which are needed here because the symbols are hard to typeset neatly in a blog's font:





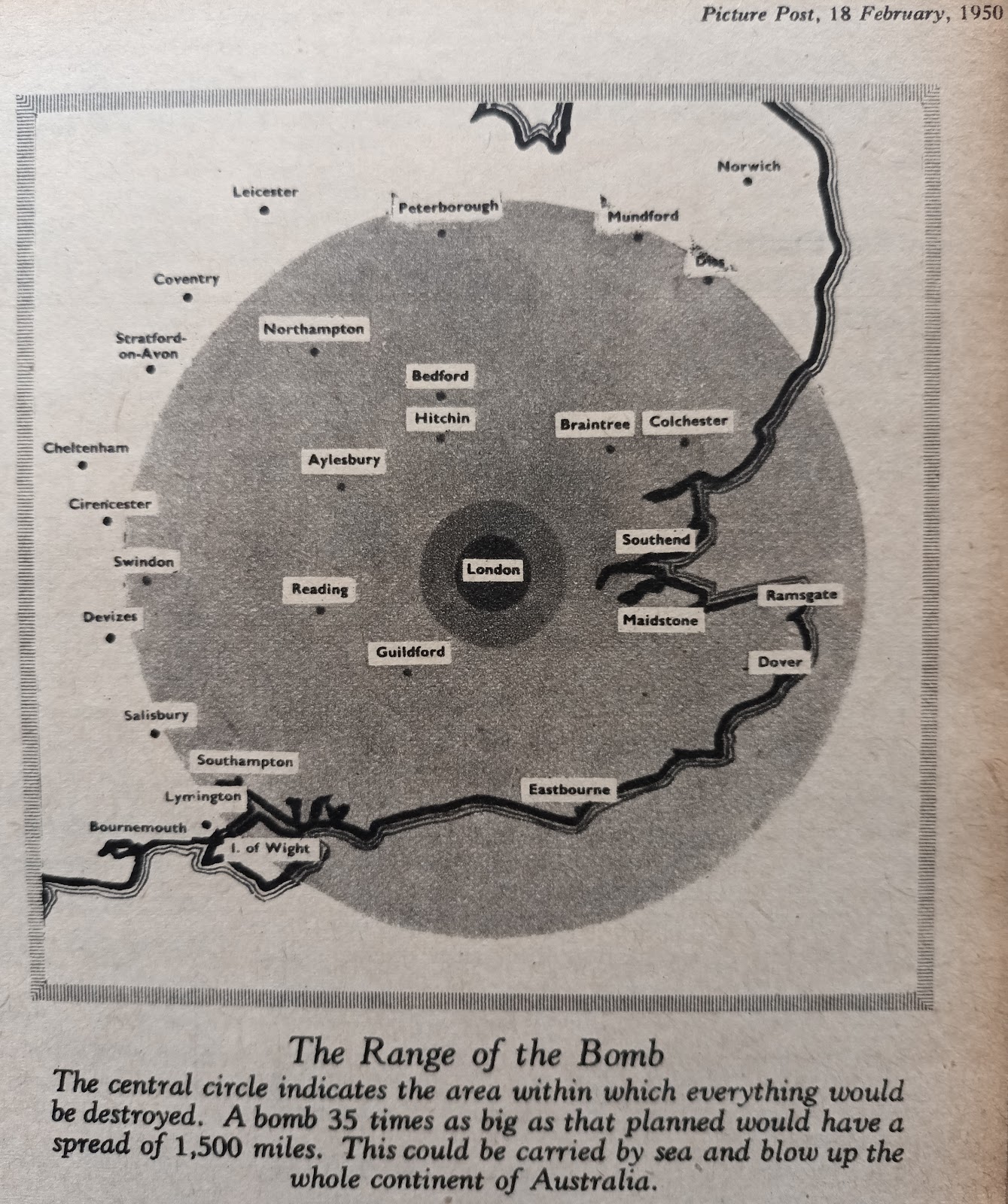


























































































































































































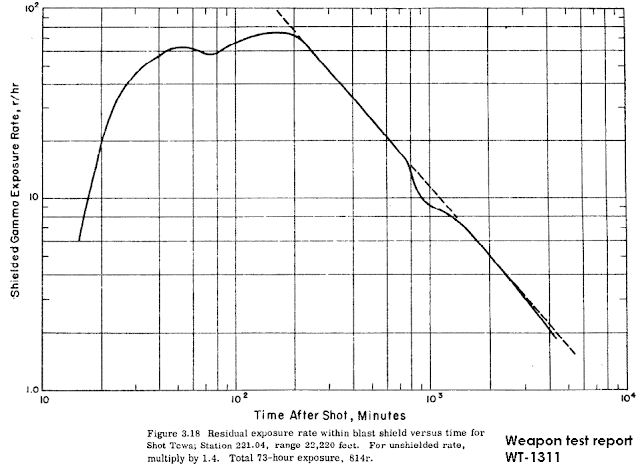
























1 Comments:
Note: there is a recent discussion of blast wave attenuation by modern cities in the comments section of the post:
http://glasstone.blogspot.co.uk/2016/03/politically-biased-science-nature-peer.html
Post a Comment
<< Home